Entropy-Regularized Partially Observed Markov Decision Processes

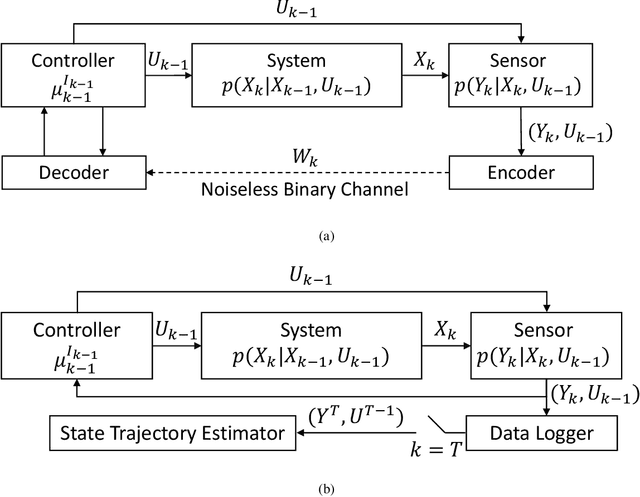
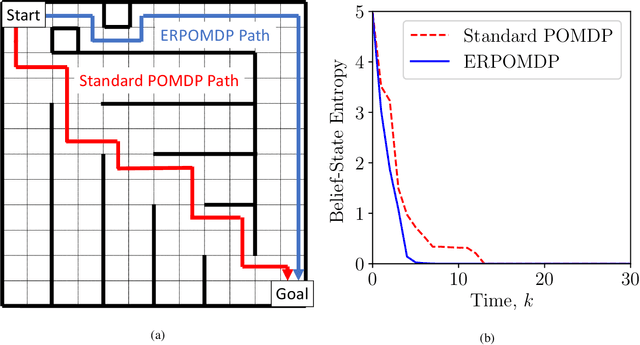
We investigate partially observed Markov decision processes (POMDPs) with cost functions regularized by entropy terms describing state, observation, and control uncertainty. Standard POMDP techniques are shown to offer bounded-error solutions to these entropy-regularized POMDPs, with exact solutions when the regularization involves the joint entropy of the state, observation, and control trajectories. Our joint-entropy result is particularly surprising since it constitutes a novel, tractable formulation of active state estimation.