Entanglement-Embedded Recurrent Network Architecture: Tensorized Latent State Propagation and Chaos Forecasting
Paper and Code
Jun 10, 2020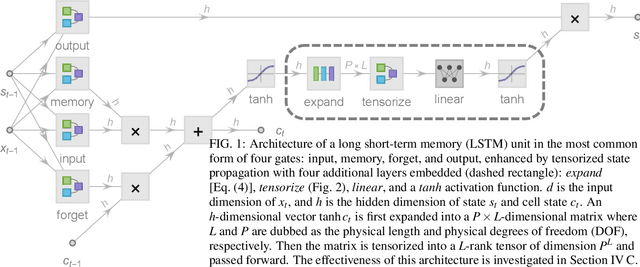
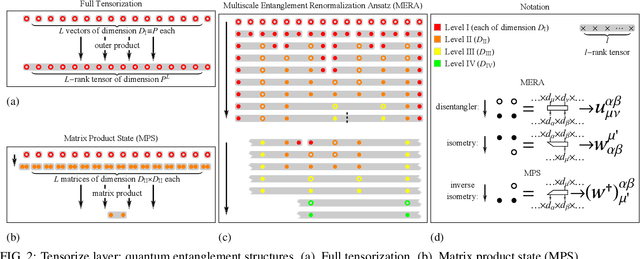
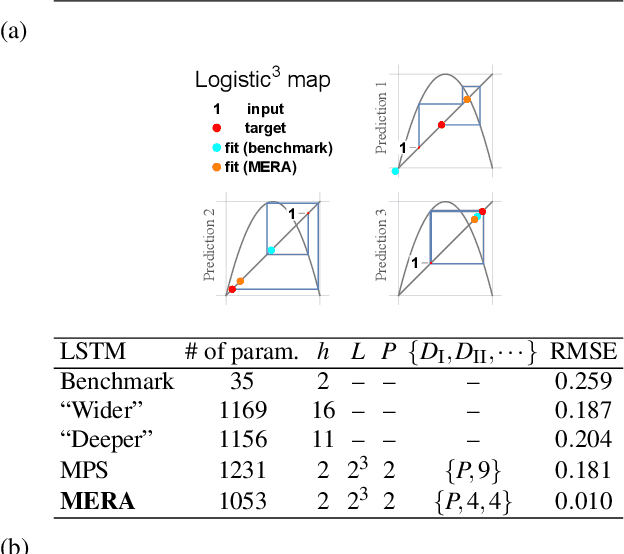
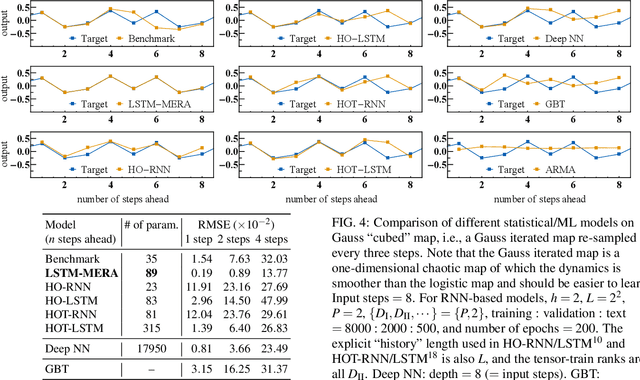
Chaotic time series forecasting has been far less understood despite its tremendous potential in theory and real-world applications. Traditional statistical/ML methods are inefficient to capture chaos in nonlinear dynamical systems, especially when the time difference $\Delta t$ between consecutive steps is so large that a trivial, ergodic local minimum would most likely be reached instead. Here, we introduce a new long-short-term-memory (LSTM)-based recurrent architecture by tensorizing the cell-state-to-state propagation therein, keeping the long-term memory feature of LSTM while simultaneously enhancing the learning of short-term nonlinear complexity. We stress that the global minima of chaos can be most efficiently reached by tensorization where all nonlinear terms, up to some polynomial order, are treated explicitly and weighted equally. The efficiency and generality of our architecture are systematically tested and confirmed by theoretical analysis and experimental results. In our design, we have explicitly used two different many-body entanglement structures---matrix product states (MPS) and the multiscale entanglement renormalization ansatz (MERA)---as physics-inspired tensor decomposition techniques, from which we find that MERA generally performs better than MPS, hence conjecturing that the learnability of chaos is determined not only by the number of free parameters but also the tensor complexity---recognized as how entanglement entropy scales with varying matricization of the tensor.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge