Ensemble Relational Learning based on Selective Propositionalization
Paper and Code
Nov 15, 2013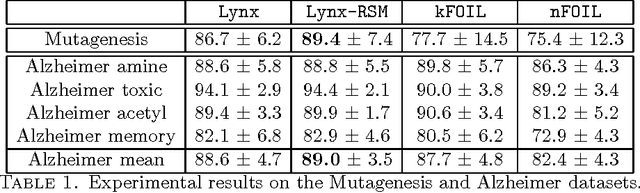
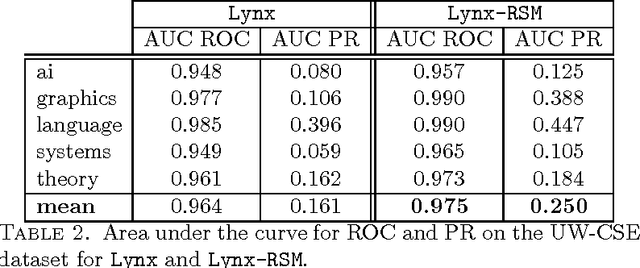

Dealing with structured data needs the use of expressive representation formalisms that, however, puts the problem to deal with the computational complexity of the machine learning process. Furthermore, real world domains require tools able to manage their typical uncertainty. Many statistical relational learning approaches try to deal with these problems by combining the construction of relevant relational features with a probabilistic tool. When the combination is static (static propositionalization), the constructed features are considered as boolean features and used offline as input to a statistical learner; while, when the combination is dynamic (dynamic propositionalization), the feature construction and probabilistic tool are combined into a single process. In this paper we propose a selective propositionalization method that search the optimal set of relational features to be used by a probabilistic learner in order to minimize a loss function. The new propositionalization approach has been combined with the random subspace ensemble method. Experiments on real-world datasets shows the validity of the proposed method.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge