Enrichment of Qualitative Beliefs for Reasoning under Uncertainty
Paper and Code
Sep 11, 2007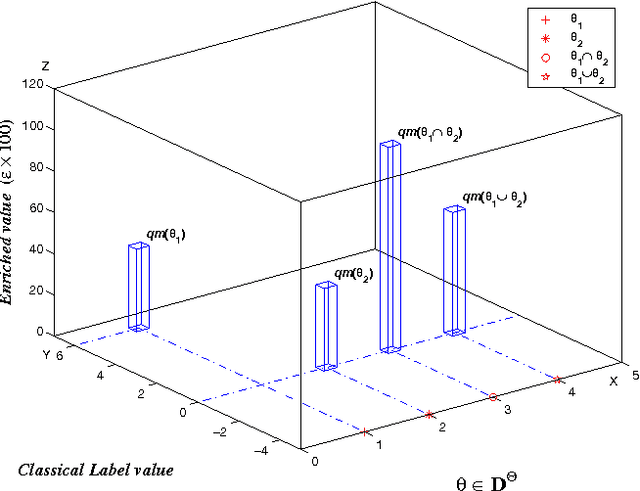
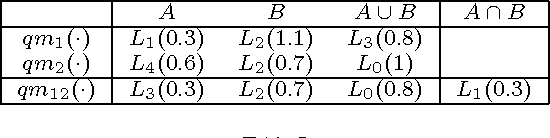
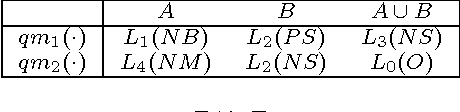

This paper deals with enriched qualitative belief functions for reasoning under uncertainty and for combining information expressed in natural language through linguistic labels. In this work, two possible enrichments (quantitative and/or qualitative) of linguistic labels are considered and operators (addition, multiplication, division, etc) for dealing with them are proposed and explained. We denote them $qe$-operators, $qe$ standing for "qualitative-enriched" operators. These operators can be seen as a direct extension of the classical qualitative operators ($q$-operators) proposed recently in the Dezert-Smarandache Theory of plausible and paradoxist reasoning (DSmT). $q$-operators are also justified in details in this paper. The quantitative enrichment of linguistic label is a numerical supporting degree in $[0,\infty)$, while the qualitative enrichment takes its values in a finite ordered set of linguistic values. Quantitative enrichment is less precise than qualitative enrichment, but it is expected more close with what human experts can easily provide when expressing linguistic labels with supporting degrees. Two simple examples are given to show how the fusion of qualitative-enriched belief assignments can be done.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge