Enhancing variational generation through self-decomposition
Paper and Code
Feb 06, 2022
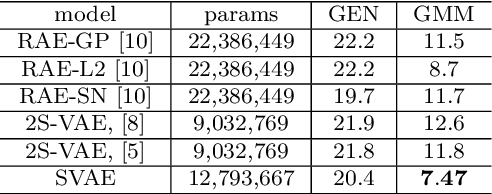


In this article we introduce the notion of Split Variational Autoencoder (SVAE), whose output $\hat{x}$ is obtained as a weighted sum $\sigma \odot \hat{x_1} + (1-\sigma) \odot \hat{x_2}$ of two generated images $\hat{x_1},\hat{x_2}$, and $\sigma$ is a learned compositional map. The network is trained as a usual Variational Autoencoder with a negative loglikelihood loss between training and reconstructed images. The decomposition is nondeterministic, but follows two main schemes, that we may roughly categorize as either "syntactic" or "semantic". In the first case, the map tends to exploit the strong correlation between adjacent pixels, splitting the image in two complementary high frequency sub-images. In the second case, the map typically focuses on the contours of objects, splitting the image in interesting variations of its content, with more marked and distinctive features. In this case, the Fr\'echet Inception Distance (FID) of $\hat{x_1}$ and $\hat{x_2}$ is usually lower (hence better) than that of $\hat{x}$, that clearly suffers from being the average of the formers. In a sense, a SVAE forces the Variational Autoencoder to {\em make choices}, in contrast with its intrinsic tendency to average between alternatives with the aim to minimize the reconstruction loss towards a specific sample. According to the FID metric, our technique, tested on typical datasets such as Mnist, Cifar10 and Celeba, allows us to outperform all previous purely variational architectures (not relying on normalization flows).
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge