Enhanced Laser-Scan Matching with Online Error Estimation for Highway and Tunnel Driving
Paper and Code
Jul 29, 2022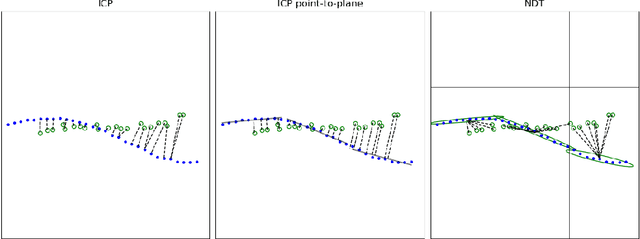

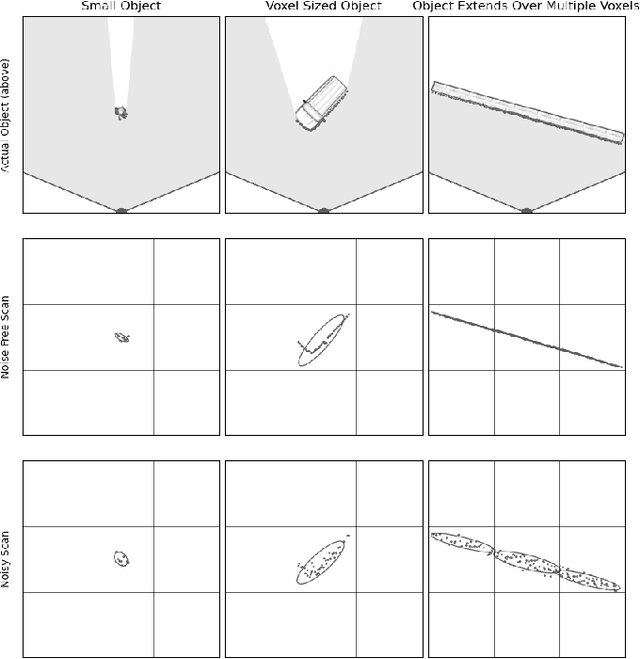
Lidar data can be used to generate point clouds for the navigation of autonomous vehicles or mobile robotics platforms. Scan matching, the process of estimating the rigid transformation that best aligns two point clouds, is the basis for lidar odometry, a form of dead reckoning. Lidar odometry is particularly useful when absolute sensors, like GPS, are not available. Here we propose the Iterative Closest Ellipsoidal Transform (ICET), a scan matching algorithm which provides two novel improvements over the current state-of-the-art Normal Distributions Transform (NDT). Like NDT, ICET decomposes lidar data into voxels and fits a Gaussian distribution to the points within each voxel. The first innovation of ICET reduces geometric ambiguity along large flat surfaces by suppressing the solution along those directions. The second innovation of ICET is to infer the output error covariance associated with the position and orientation transformation between successive point clouds; the error covariance is particularly useful when ICET is incorporated into a state-estimation routine such as an extended Kalman filter. We constructed a simulation to compare the performance of ICET and NDT in 2D space both with and without geometric ambiguity and found that ICET produces superior estimates while accurately predicting solution accuracy.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge