Empirical Loss Landscape Analysis of Neural Network Activation Functions
Paper and Code
Jun 28, 2023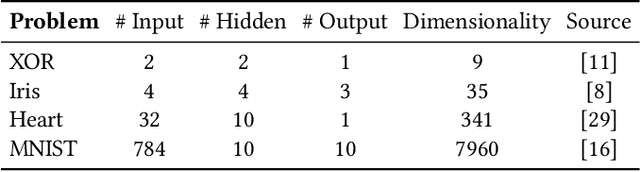
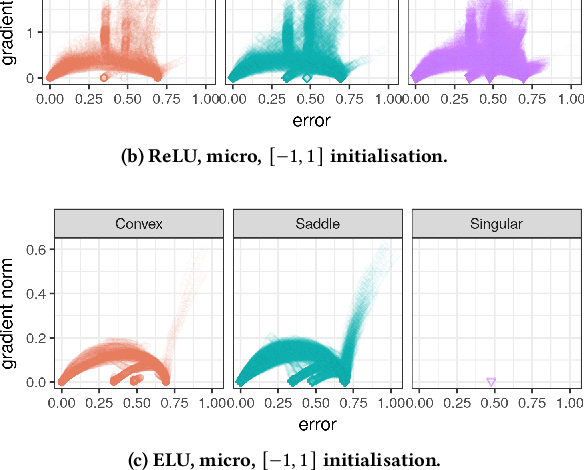
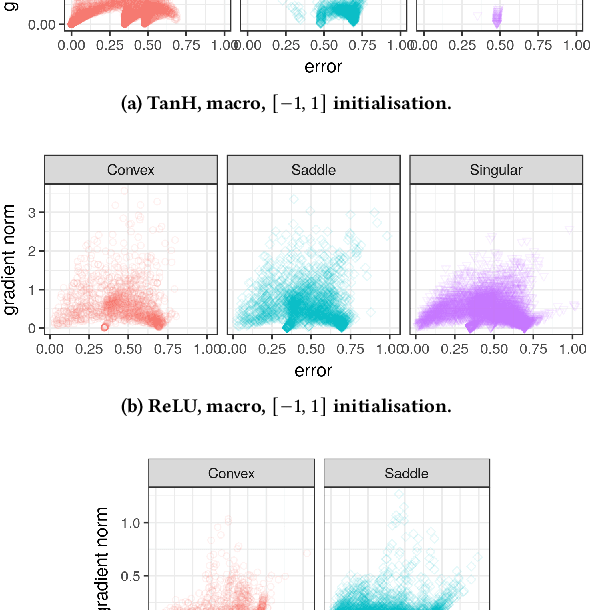
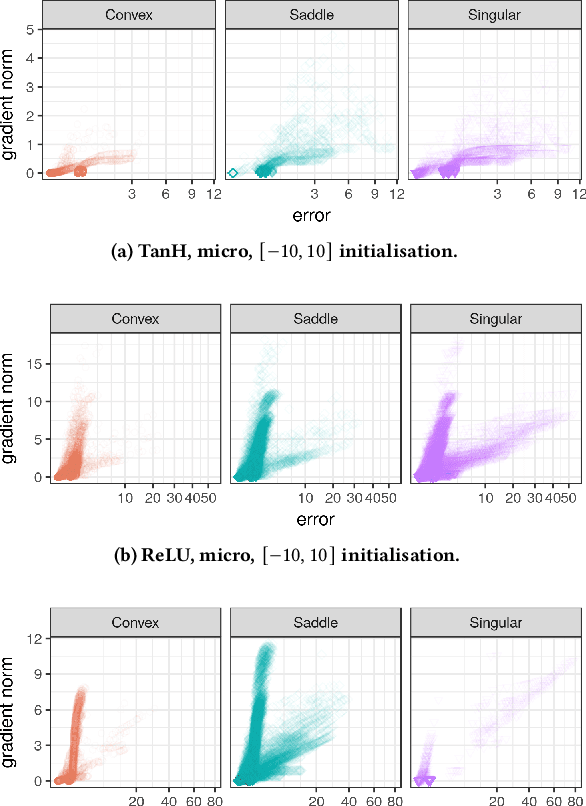
Activation functions play a significant role in neural network design by enabling non-linearity. The choice of activation function was previously shown to influence the properties of the resulting loss landscape. Understanding the relationship between activation functions and loss landscape properties is important for neural architecture and training algorithm design. This study empirically investigates neural network loss landscapes associated with hyperbolic tangent, rectified linear unit, and exponential linear unit activation functions. Rectified linear unit is shown to yield the most convex loss landscape, and exponential linear unit is shown to yield the least flat loss landscape, and to exhibit superior generalisation performance. The presence of wide and narrow valleys in the loss landscape is established for all activation functions, and the narrow valleys are shown to correlate with saturated neurons and implicitly regularised network configurations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge