Eliminating Unfounded Set Checking for HEX-Programs
Paper and Code
Jan 08, 2013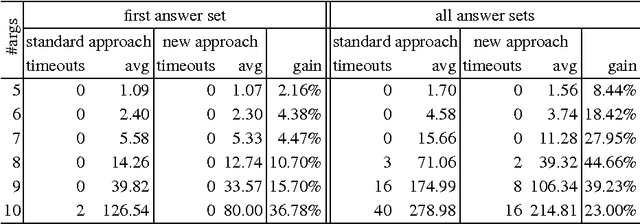
HEX-programs are an extension of the Answer Set Programming (ASP) paradigm incorporating external means of computation into the declarative programming language through so-called external atoms. Their semantics is defined in terms of minimal models of the Faber-Leone-Pfeifer (FLP) reduct. Developing native solvers for HEX-programs based on an appropriate notion of unfounded sets has been subject to recent research for reasons of efficiency. Although this has lead to an improvement over naive minimality checking using the FLP reduct, testing for foundedness remains a computationally expensive task. In this work we improve on HEX-program evaluation in this respect by identifying a syntactic class of programs, that can be efficiently recognized and allows to entirely skip the foundedness check. Moreover, we develop criteria for decomposing a program into components, such that the search for unfounded sets can be restricted. Observing that our results apply to many HEX-program applications provides analytic evidence for the significance and effectiveness of our approach, which is complemented by a brief discussion of preliminary experimental validation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge