Eliminating Ratio Bias for Gradient-based Simulated Parameter Estimation
Paper and Code
Nov 20, 2024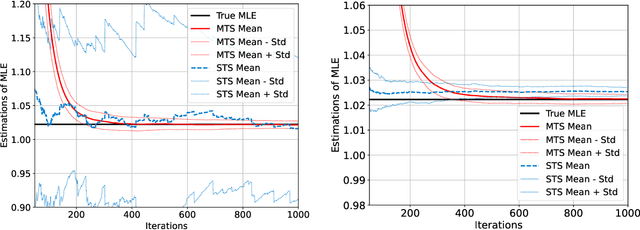

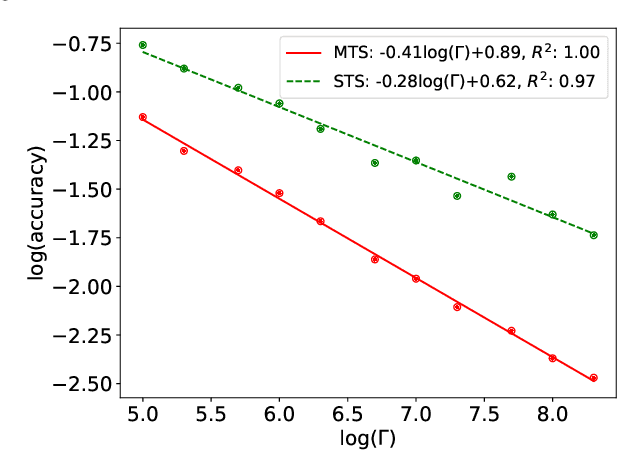
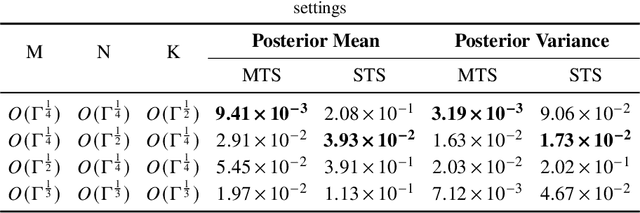
This article addresses the challenge of parameter calibration in stochastic models where the likelihood function is not analytically available. We propose a gradient-based simulated parameter estimation framework, leveraging a multi-time scale algorithm that tackles the issue of ratio bias in both maximum likelihood estimation and posterior density estimation problems. Additionally, we introduce a nested simulation optimization structure, providing theoretical analyses including strong convergence, asymptotic normality, convergence rate, and budget allocation strategies for the proposed algorithm. The framework is further extended to neural network training, offering a novel perspective on stochastic approximation in machine learning. Numerical experiments show that our algorithm can improve the estimation accuracy and save computational costs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge