ELF: Exact-Lipschitz Based Universal Density Approximator Flow
Paper and Code
Dec 13, 2021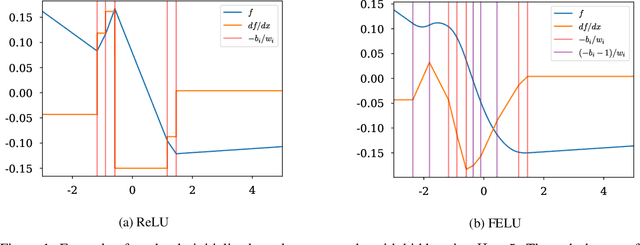
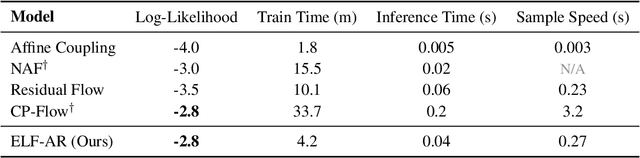
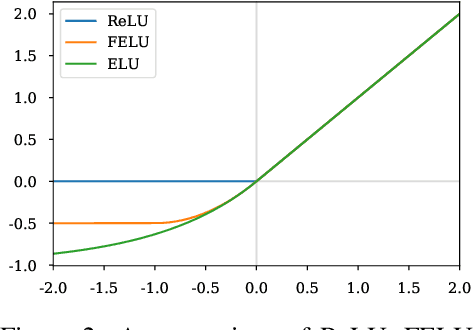
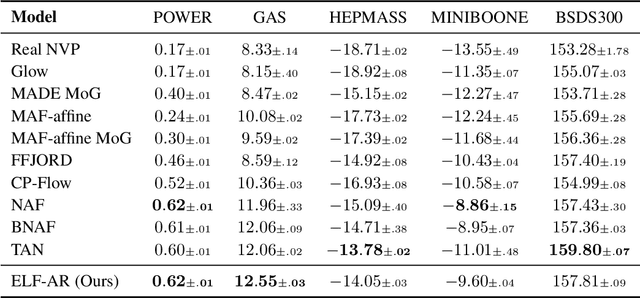
Normalizing flows have grown more popular over the last few years; however, they continue to be computationally expensive, making them difficult to be accepted into the broader machine learning community. In this paper, we introduce a simple one-dimensional one-layer network that has closed form Lipschitz constants; using this, we introduce a new Exact-Lipschitz Flow (ELF) that combines the ease of sampling from residual flows with the strong performance of autoregressive flows. Further, we show that ELF is provably a universal density approximator, more computationally and parameter efficient compared to a multitude of other flows, and achieves state-of-the-art performance on multiple large-scale datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge