Elementary superexpressive activations
Paper and Code
Feb 22, 2021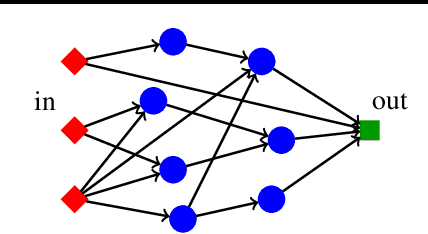
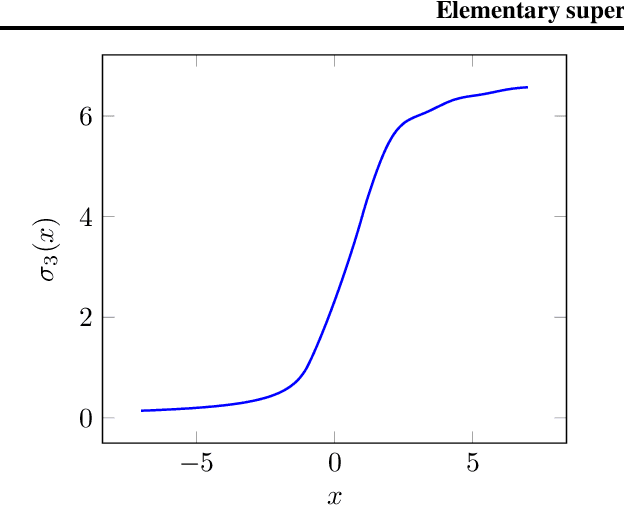
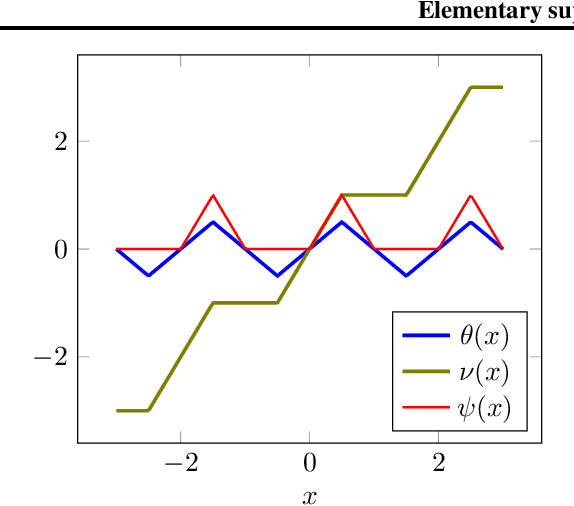
We call a finite family of activation functions superexpressive if any multivariate continuous function can be approximated by a neural network that uses these activations and has a fixed architecture only depending on the number of input variables (i.e., to achieve any accuracy we only need to adjust the weights, without increasing the number of neurons). Previously, it was known that superexpressive activations exist, but their form was quite complex. We give examples of very simple superexpressive families: for example, we prove that the family {sin, arcsin} is superexpressive. We also show that most practical activations (not involving periodic functions) are not superexpressive.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge