Electoral David vs Goliath: How does the Spatial Concentration of Electors affect District-based Elections?
Paper and Code
Jun 21, 2020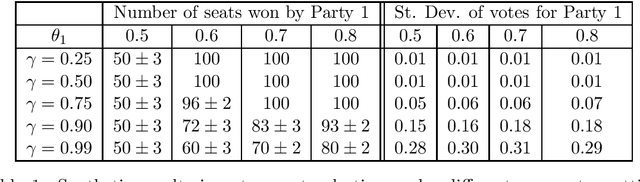
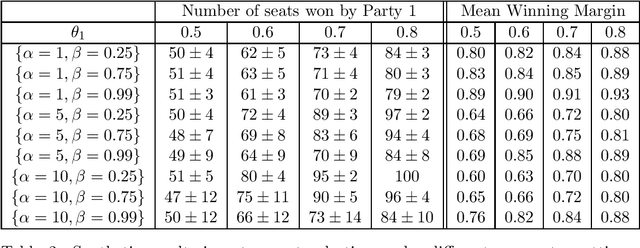
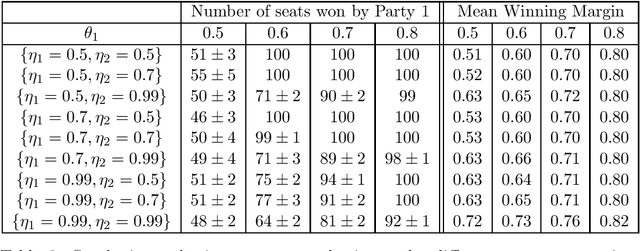
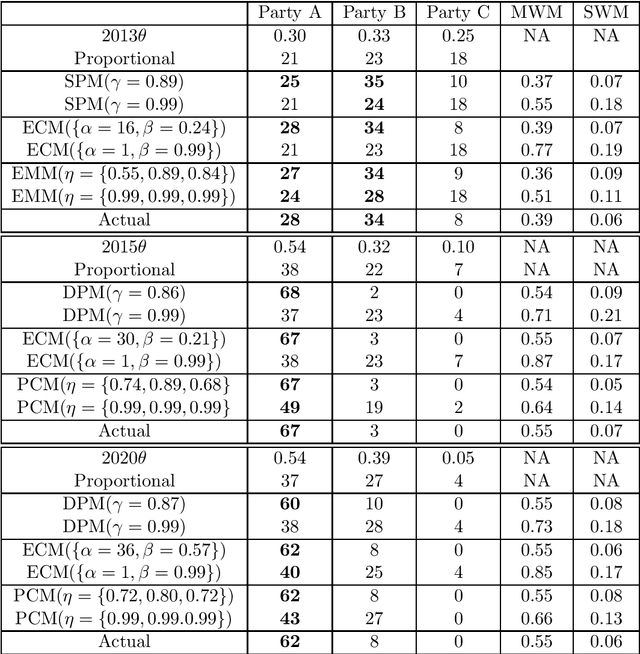
Many democratic countries use district-based elections where there is a "seat" for each district in the governing body. In each district, the party whose candidate gets the maximum number of votes wins the corresponding seat. The result of the election is decided based on the number of seats won by the different parties. The electors (voters) can cast their votes only in the district of their residence. Thus, locations of the electors and boundaries of the districts may severely affect the election result even if the proportion of popular support (number of electors) of different parties remains unchanged. This has led to significant amount of research on whether the districts may be redrawn or electors may be moved to maximize seats for a particular party. In this paper, we frame the spatial distribution of electors in a probabilistic setting, and explore different models to capture the intra-district polarization of electors in favour of a party, or the spatial concentration of supporters of different parties. Our models are inspired by elections in India, where supporters of different parties tend to be concentrated in certain districts. We show with extensive simulations that our model can capture different statistical properties of real elections held in India. We frame parameter estimation problems to fit our models to the observed election results. Since analytical calculation of the likelihood functions are infeasible for our complex models, we use Likelihood-free Inference methods under the Approximate Bayesian Computation framework. Since this approach is highly time-consuming, we explore how supervised regression using Logistic Regression or Deep Neural Networks can be used to speed it up. We also explore how the election results can change by varying the spatial distributions of the voters, even when the proportions of popular support of the parties remain constant.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge