Efficient Topology-Controlled Sampling of Implicit Shapes
Paper and Code
May 16, 2012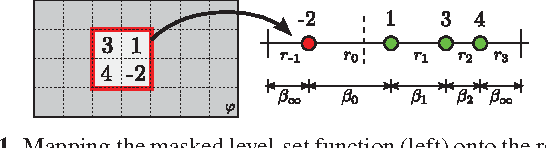
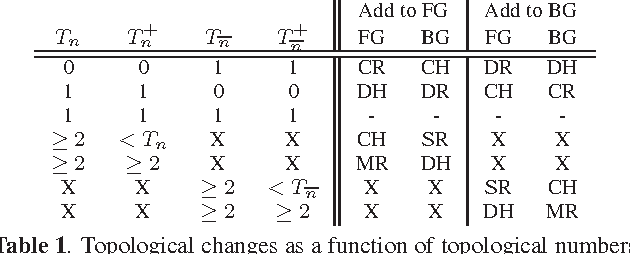
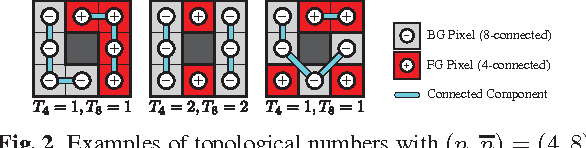

Sampling from distributions of implicitly defined shapes enables analysis of various energy functionals used for image segmentation. Recent work describes a computationally efficient Metropolis-Hastings method for accomplishing this task. Here, we extend that framework so that samples are accepted at every iteration of the sampler, achieving an order of magnitude speed up in convergence. Additionally, we show how to incorporate topological constraints.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge