Efficient inference in stochastic block models with vertex labels
Paper and Code
Aug 17, 2018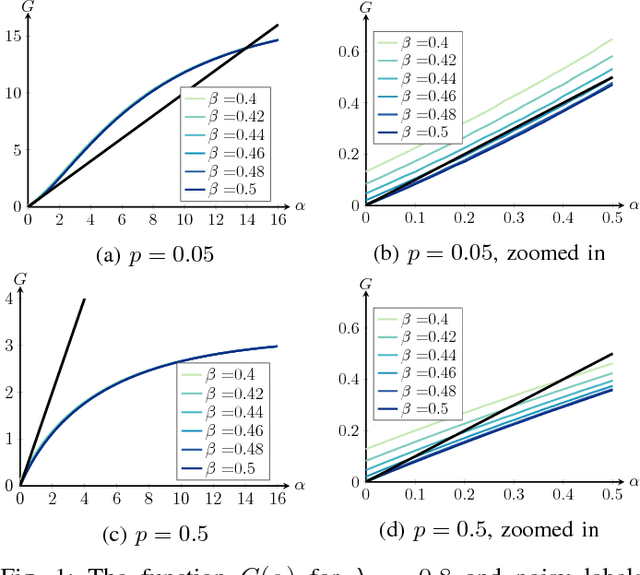
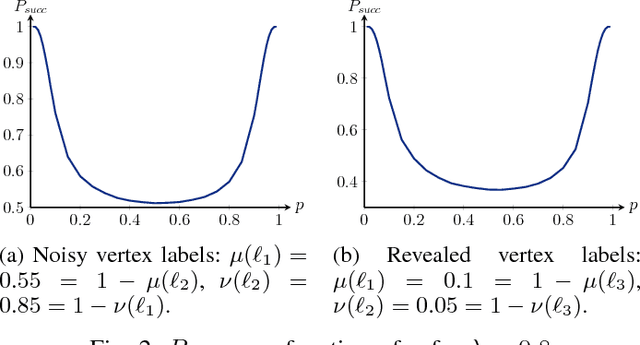
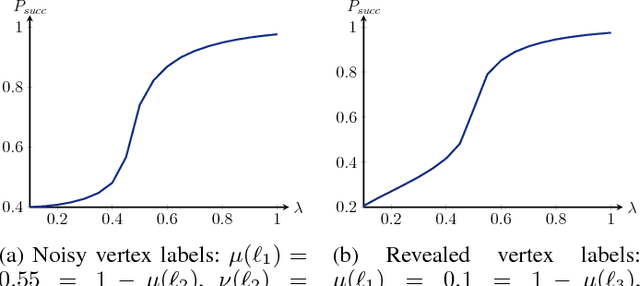
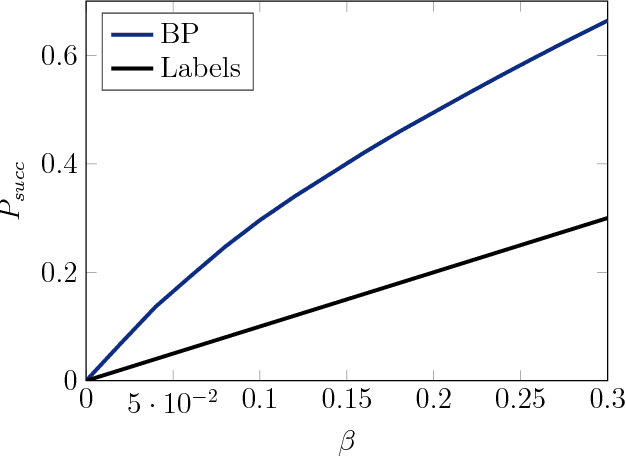
We study the stochastic block model with two communities where vertices contain side information in the form of a vertex label. These vertex labels may have arbitrary label distributions, depending on the community memberships. We analyze a linearized version of the popular belief propagation algorithm. We show that this algorithm achieves the highest accuracy possible whenever a certain function of the network parameters has a unique fixed point. Whenever this function has multiple fixed points, the belief propagation algorithm may not perform optimally. We show that increasing the information in the vertex labels may reduce the number of fixed points and hence lead to optimality of belief propagation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge