Efficient Hyperparameter Tuning with Dynamic Accuracy Derivative-Free Optimization
Paper and Code
Nov 06, 2020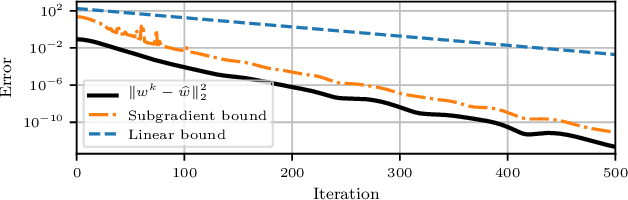
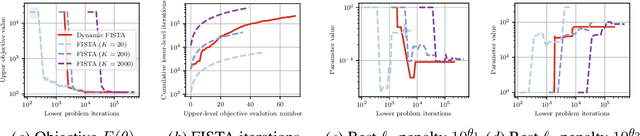


Many machine learning solutions are framed as optimization problems which rely on good hyperparameters. Algorithms for tuning these hyperparameters usually assume access to exact solutions to the underlying learning problem, which is typically not practical. Here, we apply a recent dynamic accuracy derivative-free optimization method to hyperparameter tuning, which allows inexact evaluations of the learning problem while retaining convergence guarantees. We test the method on the problem of learning elastic net weights for a logistic classifier, and demonstrate its robustness and efficiency compared to a fixed accuracy approach. This demonstrates a promising approach for hyperparameter tuning, with both convergence guarantees and practical performance.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge