Efficient Exploration for Model-based Reinforcement Learning with Continuous States and Actions
Paper and Code
Nov 20, 2020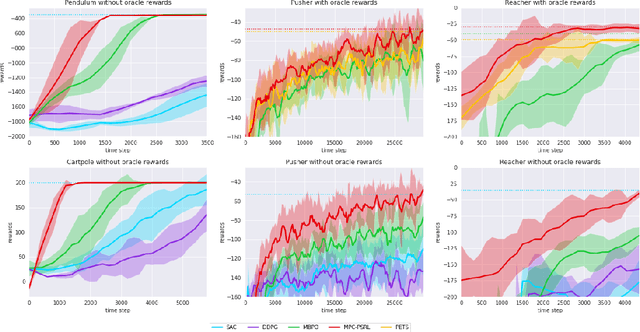
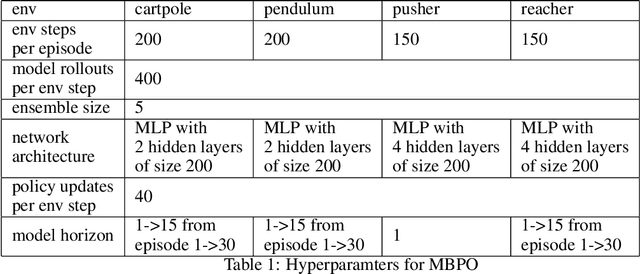
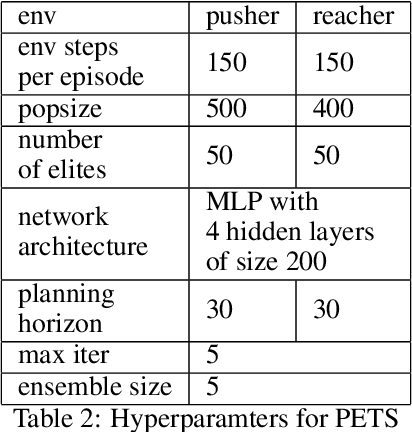
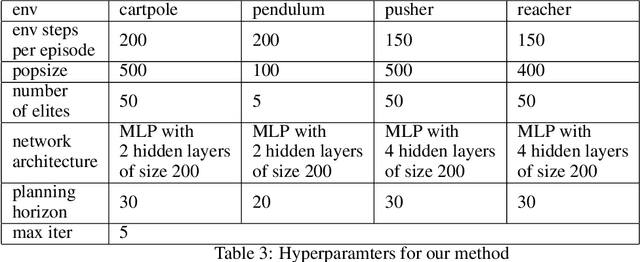
Balancing exploration and exploitation is crucial in reinforcement learning (RL). In this paper, we study the model-based posterior sampling algorithm in continuous state-action spaces theoretically and empirically. First, we improve the regret bound: with the assumption that reward and transition functions can be modeled as Gaussian Processes with linear kernels, we develop a Bayesian regret bound of $\tilde{O}(H^{3/2}d\sqrt{T})$, where $H$ is the episode length, $d$ is the dimension of the state-action space, and $T$ indicates the total time steps. Our bound can be extended to nonlinear cases as well: using linear kernels on the feature representation $\phi$, the Bayesian regret bound becomes $\tilde{O}(H^{3/2}d_{\phi}\sqrt{T})$, where $d_\phi$ is the dimension of the representation space. Moreover, we present MPC-PSRL, a model-based posterior sampling algorithm with model predictive control for action selection. To capture the uncertainty in models and realize posterior sampling, we use Bayesian linear regression on the penultimate layer (the feature representation layer $\phi$) of neural networks. Empirical results show that our algorithm achieves the best sample efficiency in benchmark control tasks compared to prior model-based algorithms, and matches the asymptotic performance of model-free algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge