Efficient estimates of optimal transport via low-dimensional embeddings
Paper and Code
Nov 08, 2021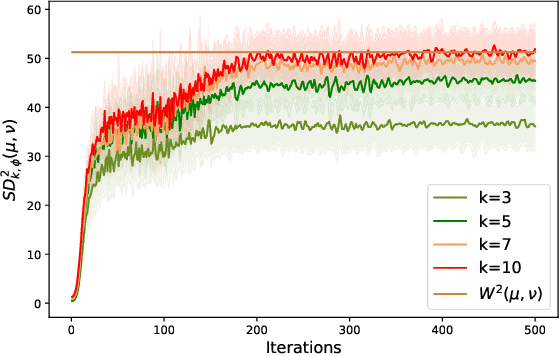
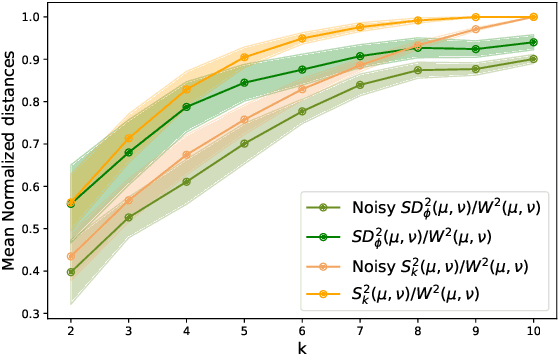
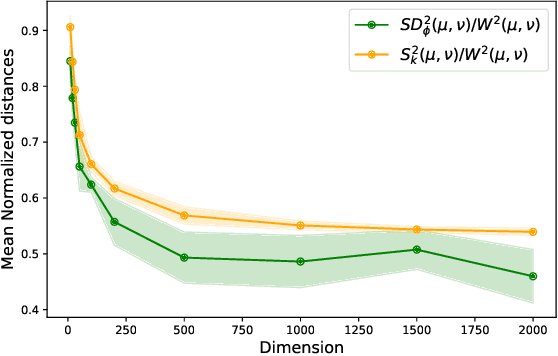
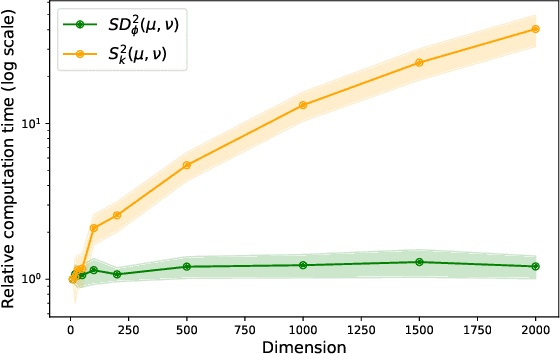
Optimal transport distances (OT) have been widely used in recent work in Machine Learning as ways to compare probability distributions. These are costly to compute when the data lives in high dimension. Recent work by Paty et al., 2019, aims specifically at reducing this cost by computing OT using low-rank projections of the data (seen as discrete measures). We extend this approach and show that one can approximate OT distances by using more general families of maps provided they are 1-Lipschitz. The best estimate is obtained by maximising OT over the given family. As OT calculations are done after mapping data to a lower dimensional space, our method scales well with the original data dimension. We demonstrate the idea with neural networks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge