Efficient computation and analysis of distributional Shapley values
Paper and Code
Jul 02, 2020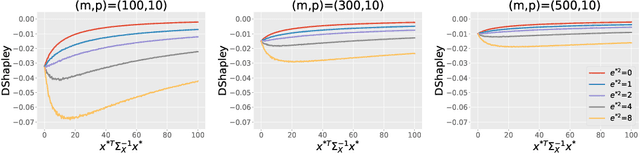
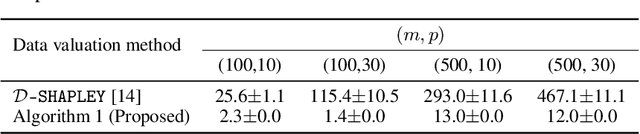
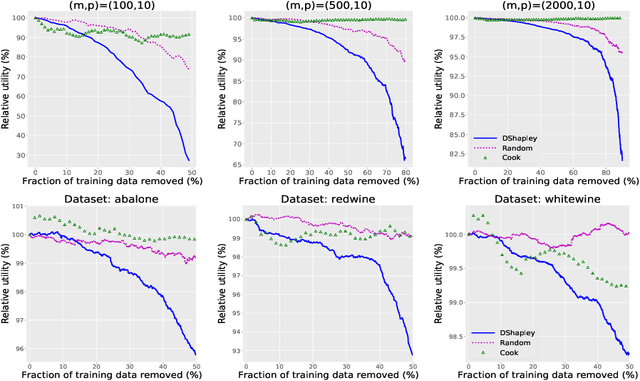
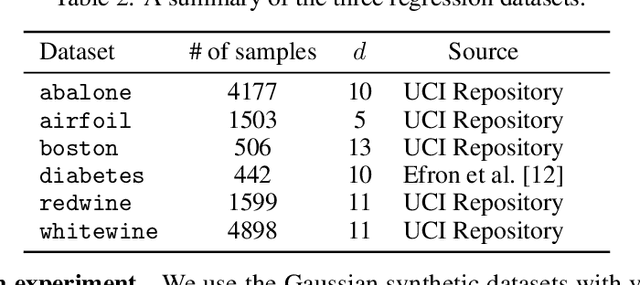
Distributional data Shapley value (DShapley) has been recently proposed as a principled framework to quantify the contribution of individual datum in machine learning. DShapley develops the foundational game theory concept of Shapley values into a statistical framework and can be applied to identify data points that are useful (or harmful) to a learning algorithm. Estimating DShapley is computationally expensive, however, and this can be a major challenge to using it in practice. Moreover, there has been little mathematical analyses of how this value depends on data characteristics. In this paper, we derive the first analytic expressions for DShapley for the canonical problems of linear regression and non-parametric density estimation. These analytic forms provide new algorithms to compute DShapley that are several orders of magnitude faster than previous state-of-the-art. Furthermore, our formulas are directly interpretable and provide quantitative insights into how the value varies for different types of data. We demonstrate the efficacy of our DShapley approach on multiple real and synthetic datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge