ECA: High Dimensional Elliptical Component Analysis in non-Gaussian Distributions

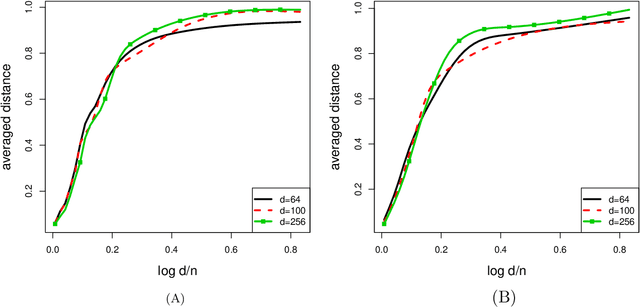
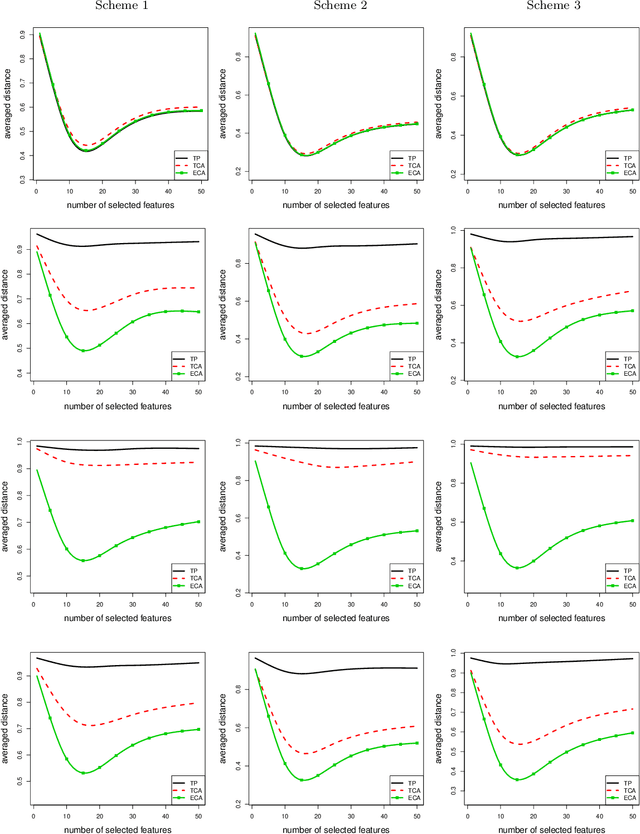
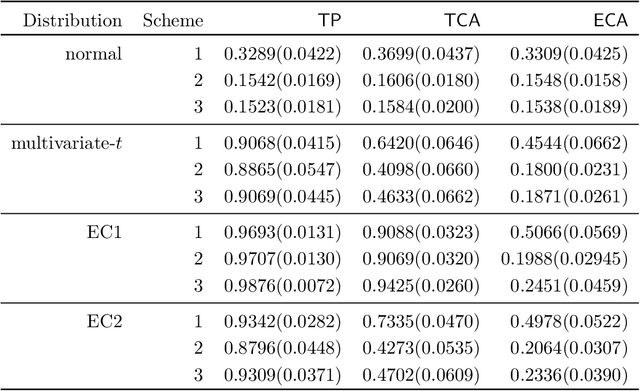
We present a robust alternative to principal component analysis (PCA) --- called elliptical component analysis (ECA) --- for analyzing high dimensional, elliptically distributed data. ECA estimates the eigenspace of the covariance matrix of the elliptical data. To cope with heavy-tailed elliptical distributions, a multivariate rank statistic is exploited. At the model-level, we consider two settings: either that the leading eigenvectors of the covariance matrix are non-sparse or that they are sparse. Methodologically, we propose ECA procedures for both non-sparse and sparse settings. Theoretically, we provide both non-asymptotic and asymptotic analyses quantifying the theoretical performances of ECA. In the non-sparse setting, we show that ECA's performance is highly related to the effective rank of the covariance matrix. In the sparse setting, the results are twofold: (i) We show that the sparse ECA estimator based on a combinatoric program attains the optimal rate of convergence; (ii) Based on some recent developments in estimating sparse leading eigenvectors, we show that a computationally efficient sparse ECA estimator attains the optimal rate of convergence under a suboptimal scaling.