Early Improving Recurrent Elastic Highway Network
Paper and Code
Aug 14, 2017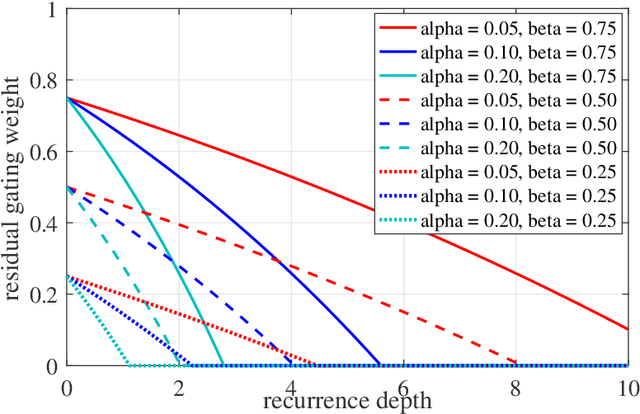
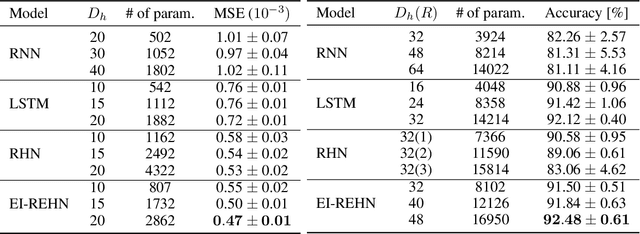
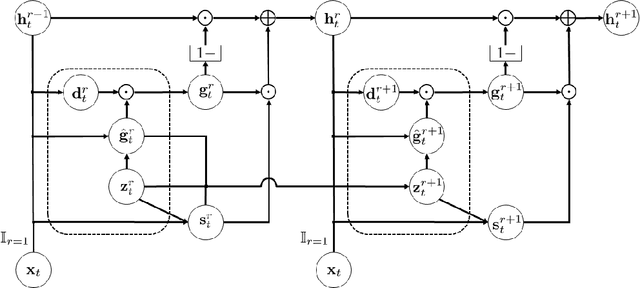

To model time-varying nonlinear temporal dynamics in sequential data, a recurrent network capable of varying and adjusting the recurrence depth between input intervals is examined. The recurrence depth is extended by several intermediate hidden state units, and the weight parameters involved in determining these units are dynamically calculated. The motivation behind the paper lies on overcoming a deficiency in Recurrent Highway Networks and improving their performances which are currently at the forefront of RNNs: 1) Determining the appropriate number of recurrent depth in RHN for different tasks is a huge burden and just setting it to a large number is computationally wasteful with possible repercussion in terms of performance degradation and high latency. Expanding on the idea of adaptive computation time (ACT), with the use of an elastic gate in the form of a rectified exponentially decreasing function taking on as arguments as previous hidden state and input, the proposed model is able to evaluate the appropriate recurrent depth for each input. The rectified gating function enables the most significant intermediate hidden state updates to come early such that significant performance gain is achieved early. 2) Updating the weights from that of previous intermediate layer offers a richer representation than the use of shared weights across all intermediate recurrence layers. The weight update procedure is just an expansion of the idea underlying hypernetworks. To substantiate the effectiveness of the proposed network, we conducted three experiments: regression on synthetic data, human activity recognition, and language modeling on the Penn Treebank dataset. The proposed networks showed better performance than other state-of-the-art recurrent networks in all three experiments.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge