Dynamic Modeling and Equilibria in Fair Decision Making
Paper and Code
Nov 15, 2019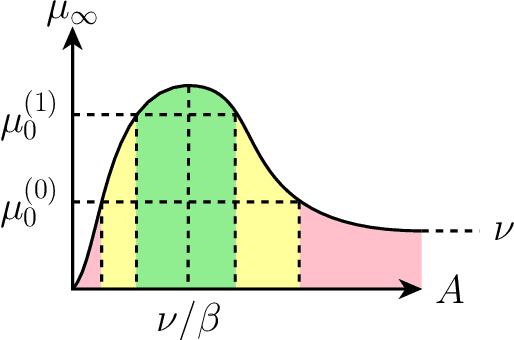
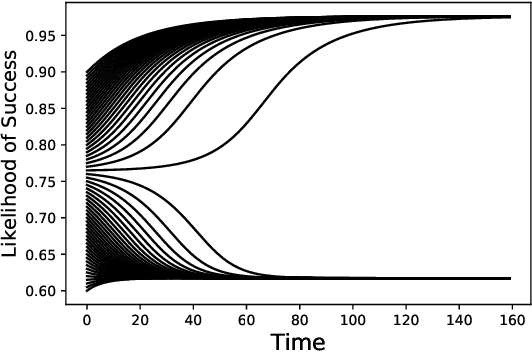
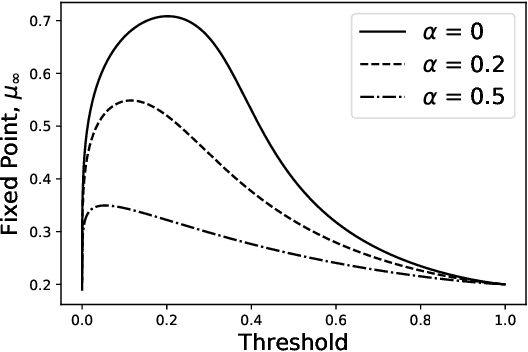
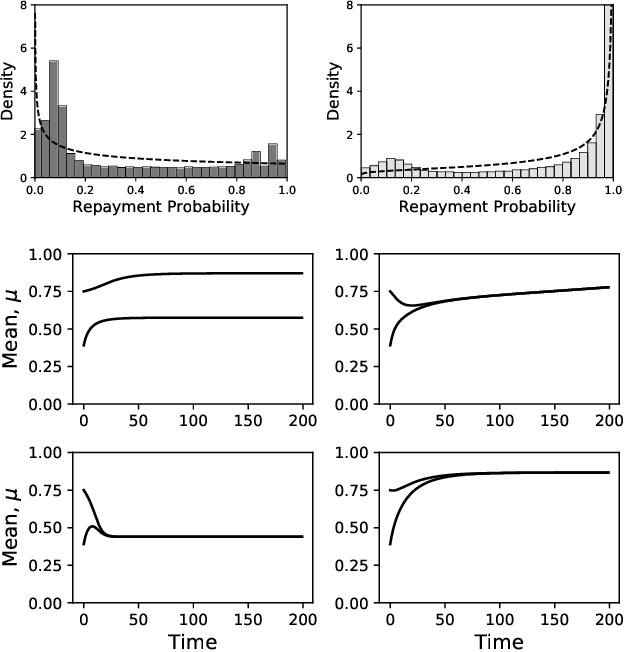
Recent studies on fairness in automated decision making systems have both investigated the potential future impact of these decisions on the population at large, and emphasized that imposing ''typical'' fairness constraints such as demographic parity or equality of opportunity does not guarantee a benefit to disadvantaged groups. However, these previous studies have focused on either simple one-step cost/benefit criteria, or on discrete underlying state spaces. In this work, we first propose a natural continuous representation of population state, governed by the Beta distribution, using a loan granting setting as a running example. Next, we apply a model of population dynamics under lending decisions, and show that when conditional payback probabilities are estimated correctly 1) ``optimal'' behavior by lenders can lead to ''Matthew Effect'' bifurcations (i.e., ''the rich get richer and the poor get poorer''), but that 2) many common fairness constraints on the allowable policies cause groups to converge to the same equilibrium point. Last, we contrast our results in the case of misspecified conditional probability estimates with prior work, and show that for this model, different levels of group misestimation guarantees that even fair policies lead to bifurcations. We illustrate some of the modeling conclusions on real data from credit scoring.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge