Dual-space Compressed Sensing
Paper and Code
Jul 15, 2022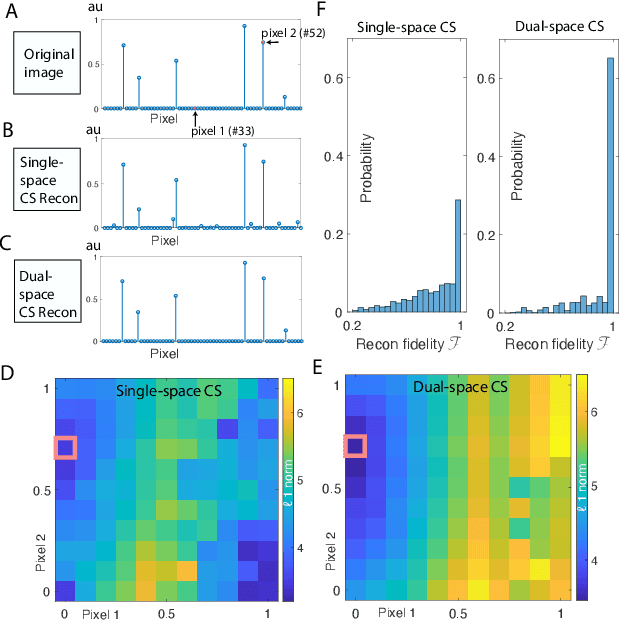
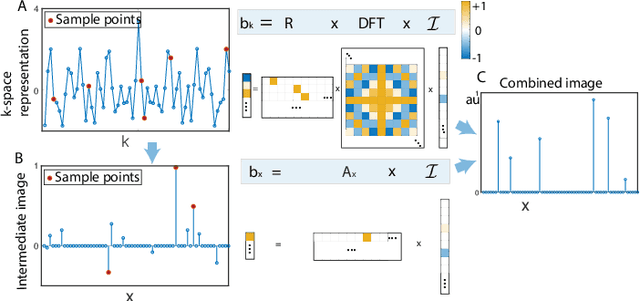
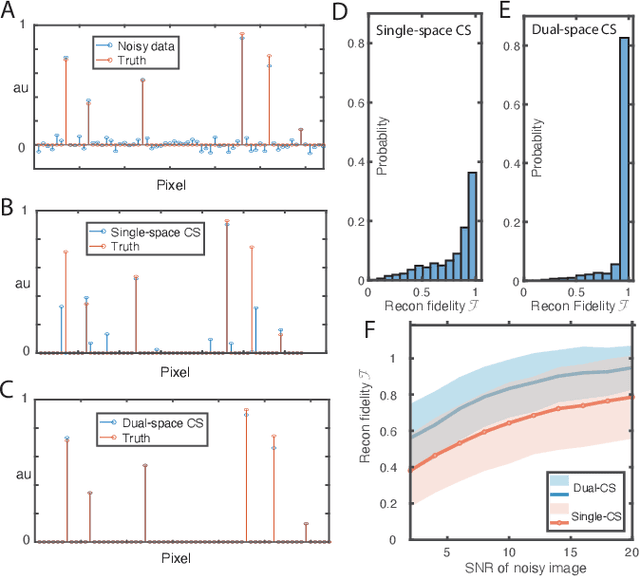
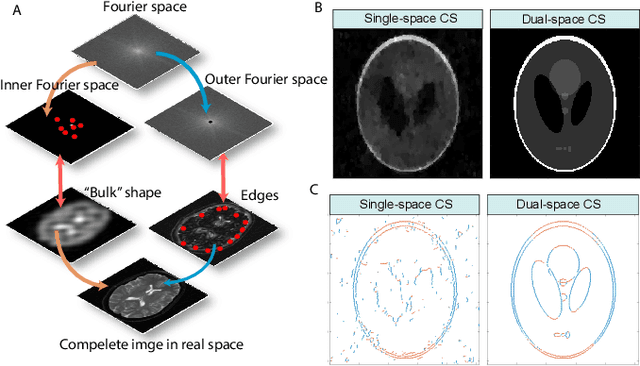
Compressed sensing (CS) is a powerful method routinely employed to accelerate image acquisition. It is particularly suited to situations when the image under consideration is sparse but can be sampled in a basis where it is non-sparse. Here we propose an alternate CS regime in situations where the image can be sampled in two incoherent spaces simultaneously, with a special focus on image sampling in Fourier reciprocal spaces (e.g. real-space and k-space). Information is fed-forward from one space to the other, allowing new opportunities to efficiently solve the optimization problem at the heart of CS image reconstruction. We show that considerable gains in imaging acceleration are then possible over conventional CS. The technique provides enhanced robustness to noise, and is well suited to edge-detection problems. We envision applications for imaging collections of nanodiamond (ND) particles targeting specific regions in a volume of interest, exploiting the ability of lattice defects (NV centers) to allow ND particles to be imaged in reciprocal spaces simultaneously via optical fluorescence and 13C magnetic resonance imaging (MRI) respectively. Broadly this work suggests the potential to interface CS principles with hybrid sampling strategies to yield speedup in signal acquisition in many practical settings.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge