DoF Analysis for -Channels through a Number-Filling Puzzle

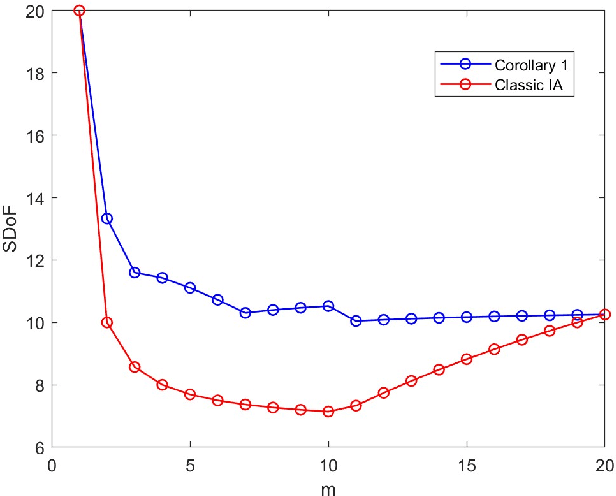
We consider a $\sf K$ user interference network with general connectivity, described by a matrix $\mat{N}$, and general message flows, described by a matrix $\mat{M}$. Previous studies have demonstrated that the standard interference scheme (IA) might not be optimal for networks with sparse connectivity. In this paper, we formalize a general IA coding scheme and an intuitive number-filling puzzle for given $\mat{M}$ and $\mat{N}$ in a way that the score of the solution to the puzzle determines the optimum sum degrees that can be achieved by the IA scheme. A solution to the puzzle is proposed for a general class of symmetric channels, and it is shown that this solution leads to significantly higher $\SDoF$ than the standard IA scheme.