Distributed Robust Principal Analysis
Paper and Code
Jul 24, 2022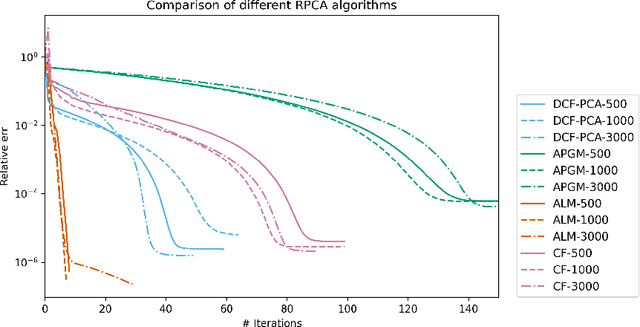
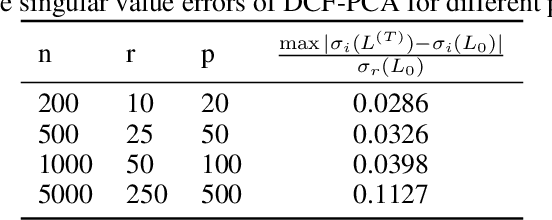
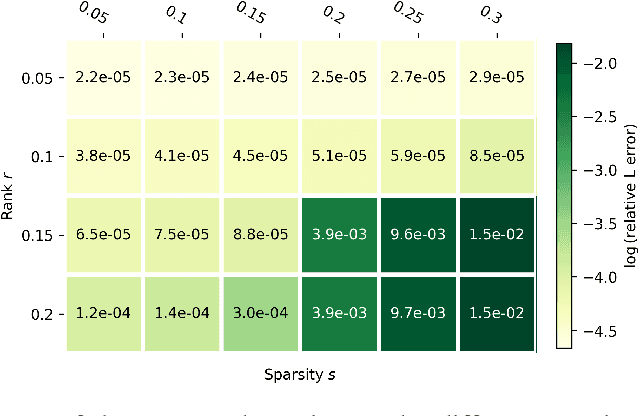
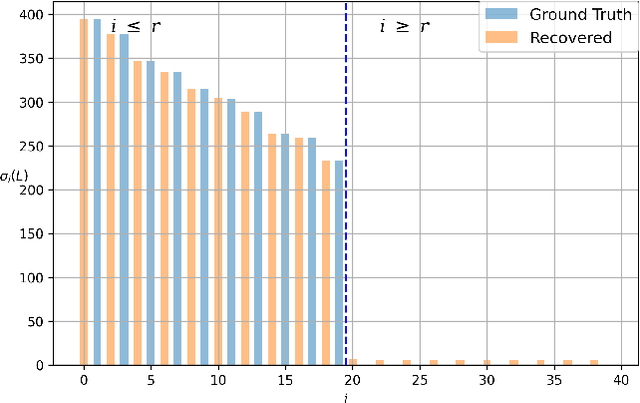
We study the robust principal component analysis (RPCA) problem in a distributed setting. The goal of RPCA is to find an underlying low-rank estimation for a raw data matrix when the data matrix is subject to the corruption of gross sparse errors. Previous studies have developed RPCA algorithms that provide stable solutions with fast convergence. However, these algorithms are typically hard to scale and cannot be implemented distributedly, due to the use of either SVD or large matrix multiplication. In this paper, we propose the first distributed robust principal analysis algorithm based on consensus factorization, dubbed DCF-PCA. We prove the convergence of DCF-PCA and evaluate DCF-PCA on various problem setting
* 13 pages
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge