Distributed Probabilistic Bisection Search using Social Learning
Paper and Code
Dec 28, 2016
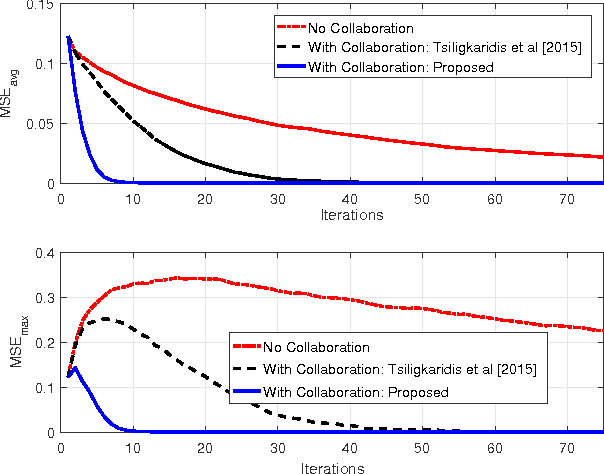

We present a novel distributed probabilistic bisection algorithm using social learning with application to target localization. Each agent in the network first constructs a query about the target based on its local information and obtains a noisy response. Agents then perform a Bayesian update of their beliefs followed by an averaging of the log beliefs over local neighborhoods. This two stage algorithm consisting of repeated querying and averaging runs until convergence. We derive bounds on the rate of convergence of the beliefs at the correct target location. Numerical simulations show that our method outperforms current state of the art methods.
* 5 Pages, Accepted to ICASSP 2017
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge