Distributed Methods with Absolute Compression and Error Compensation

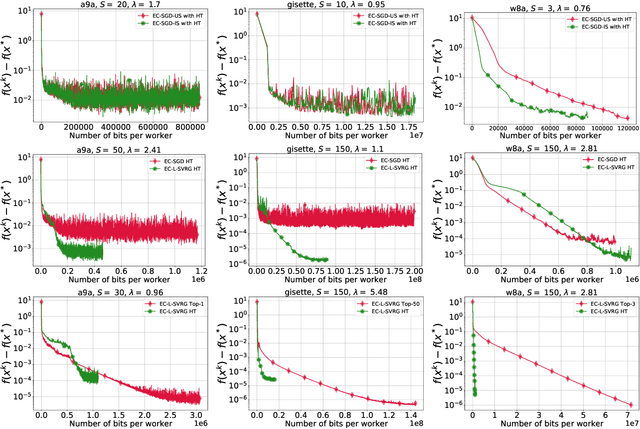
Distributed optimization methods are often applied to solving huge-scale problems like training neural networks with millions and even billions of parameters. In such applications, communicating full vectors, e.g., (stochastic) gradients, iterates, is prohibitively expensive, especially when the number of workers is large. Communication compression is a powerful approach to alleviating this issue, and, in particular, methods with biased compression and error compensation are extremely popular due to their practical efficiency. Sahu et al. (2021) propose a new analysis of Error Compensated SGD (EC-SGD) for the class of absolute compression operators showing that in a certain sense, this class contains optimal compressors for EC-SGD. However, the analysis was conducted only under the so-called $(M,\sigma^2)$-bounded noise assumption. In this paper, we generalize the analysis of EC-SGD with absolute compression to the arbitrary sampling strategy and propose the first analysis of EC-LSVRG with absolute compression for (strongly) convex problems. Our rates improve upon the previously known ones in this setting. Our theoretical findings are corroborated by several numerical experiments.