Discrete Denoising Flows
Paper and Code
Jul 24, 2021

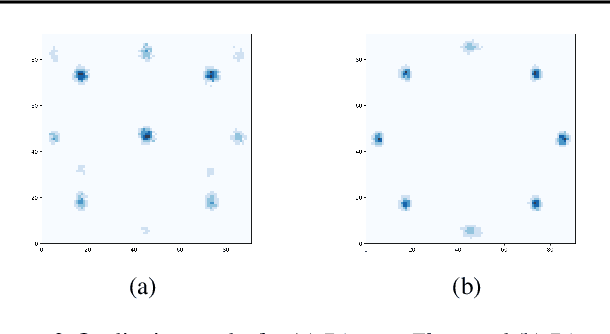
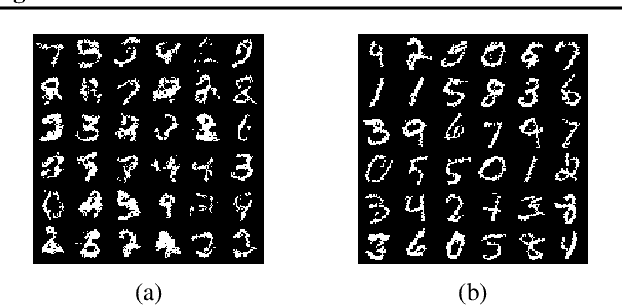
Discrete flow-based models are a recently proposed class of generative models that learn invertible transformations for discrete random variables. Since they do not require data dequantization and maximize an exact likelihood objective, they can be used in a straight-forward manner for lossless compression. In this paper, we introduce a new discrete flow-based model for categorical random variables: Discrete Denoising Flows (DDFs). In contrast with other discrete flow-based models, our model can be locally trained without introducing gradient bias. We show that DDFs outperform Discrete Flows on modeling a toy example, binary MNIST and Cityscapes segmentation maps, measured in log-likelihood.
* Accepted to the Third workshop on Invertible Neural Networks,
Normalizing Flows, and Explicit Likelihood Models (ICML 2021)
View paper on
 OpenReview
OpenReview
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge