Direct high-order edge-preserving regularization for tomographic image reconstruction
Paper and Code
Sep 15, 2015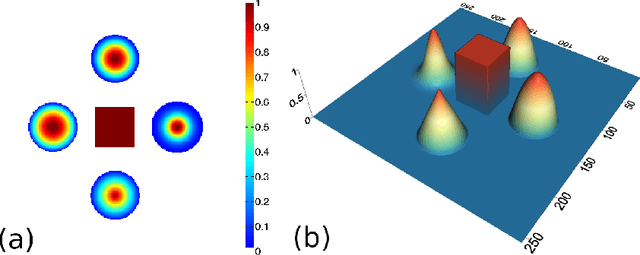

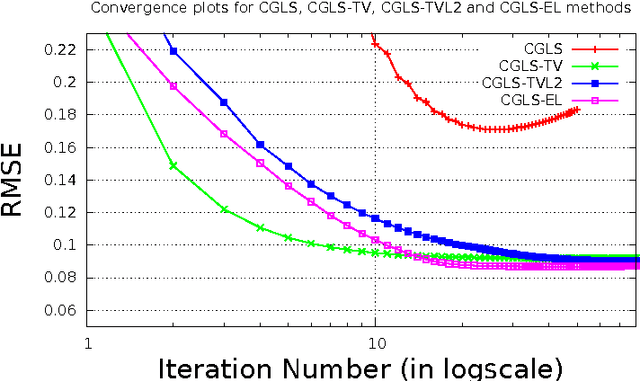
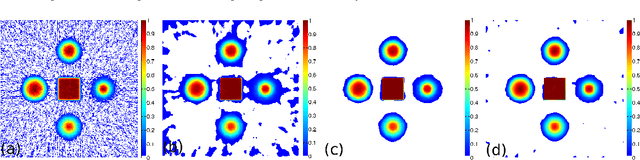
In this paper we present a new two-level iterative algorithm for tomographic image reconstruction. The algorithm uses a regularization technique, which we call edge-preserving Laplacian, that preserves sharp edges between objects while damping spurious oscillations in the areas where the reconstructed image is smooth. Our numerical simulations demonstrate that the proposed method outperforms total variation (TV) regularization and it is competitive with the combined TV-L2 penalty. Obtained reconstructed images show increased signal-to-noise ratio and visually appealing structural features. Computer implementation and parameter control of the proposed technique is straightforward, which increases the feasibility of it across many tomographic applications. In this paper, we applied our method to the under-sampled computed tomography (CT) projection data and also considered a case of reconstruction in emission tomography The MATLAB code is provided to support obtained results.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge