Differentially Private Analysis of Outliers
Paper and Code
Jul 27, 2015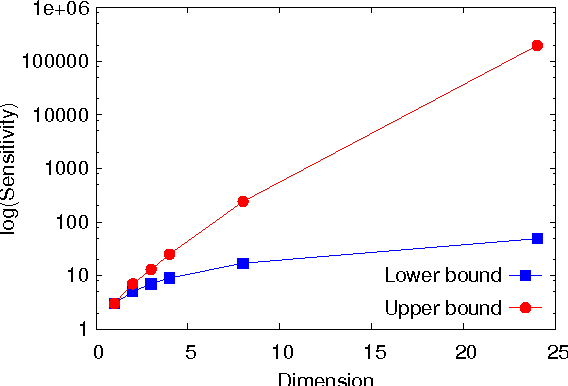
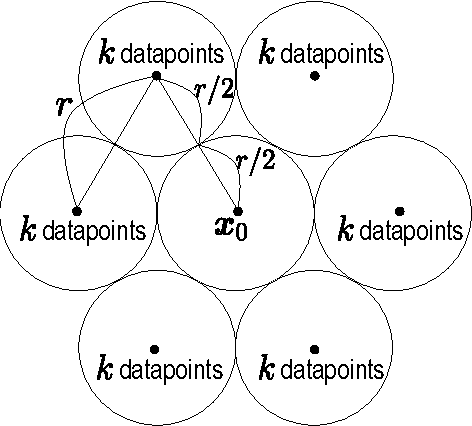


This paper investigates differentially private analysis of distance-based outliers. The problem of outlier detection is to find a small number of instances that are apparently distant from the remaining instances. On the other hand, the objective of differential privacy is to conceal presence (or absence) of any particular instance. Outlier detection and privacy protection are thus intrinsically conflicting tasks. In this paper, instead of reporting outliers detected, we present two types of differentially private queries that help to understand behavior of outliers. One is the query to count outliers, which reports the number of outliers that appear in a given subspace. Our formal analysis on the exact global sensitivity of outlier counts reveals that regular global sensitivity based method can make the outputs too noisy, particularly when the dimensionality of the given subspace is high. Noting that the counts of outliers are typically expected to be relatively small compared to the number of data, we introduce a mechanism based on the smooth upper bound of the local sensitivity. The other is the query to discovery top-$h$ subspaces containing a large number of outliers. This task can be naively achieved by issuing count queries to each subspace in turn. However, the variation of subspaces can grow exponentially in the data dimensionality. This can cause serious consumption of the privacy budget. For this task, we propose an exponential mechanism with a customized score function for subspace discovery. To the best of our knowledge, this study is the first trial to ensure differential privacy for distance-based outlier analysis. We demonstrated our methods with synthesized datasets and real datasets. The experimental results show that out method achieve better utility compared to the global sensitivity based methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge