Differential Equations for Continuous-Time Deep Learning
Paper and Code
Jan 08, 2024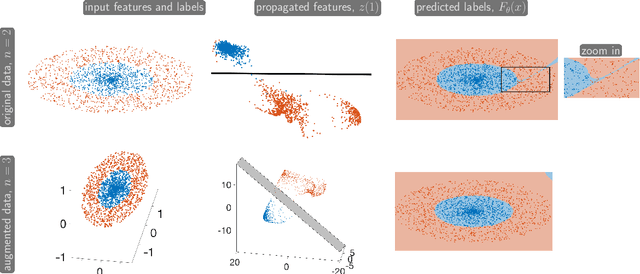
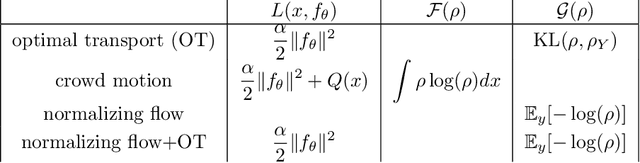
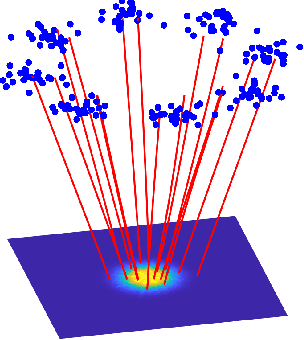
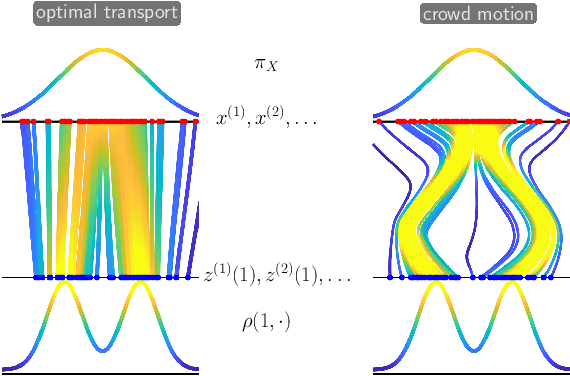
This short, self-contained article seeks to introduce and survey continuous-time deep learning approaches that are based on neural ordinary differential equations (neural ODEs). It primarily targets readers familiar with ordinary and partial differential equations and their analysis who are curious to see their role in machine learning. Using three examples from machine learning and applied mathematics, we will see how neural ODEs can provide new insights into deep learning and a foundation for more efficient algorithms.
* A version of this article is under review at AMS Notices. 10 pages, 3
figures
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge