Differentiable Topology Estimating from Curvatures for 3D Shapes
Paper and Code
Nov 28, 2024

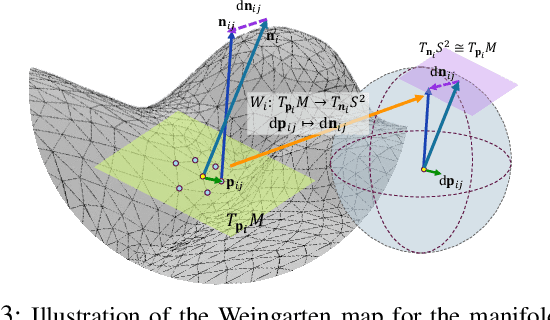

In the field of data-driven 3D shape analysis and generation, the estimation of global topological features from localized representations such as point clouds, voxels, and neural implicit fields is a longstanding challenge. This paper introduces a novel, differentiable algorithm tailored to accurately estimate the global topology of 3D shapes, overcoming the limitations of traditional methods rooted in mesh reconstruction and topological data analysis. The proposed method ensures high accuracy, efficiency, and instant computation with GPU compatibility. It begins with an efficient calculation of the self-adjoint Weingarten map for point clouds and its adaptations for other modalities. The curvatures are then extracted, and their integration over tangent differentiable Voronoi elements is utilized to estimate key topological invariants, including the Euler number and Genus. Additionally, an auto-optimization mechanism is implemented to refine the local moving frames and area elements based on the integrity of topological invariants. Experimental results demonstrate the method's superior performance across various datasets. The robustness and differentiability of the algorithm ensure its seamless integration into deep learning frameworks, offering vast potential for downstream tasks in 3D shape analysis.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge