Differentiable Boustrophedon Path Plans
Paper and Code
Sep 18, 2023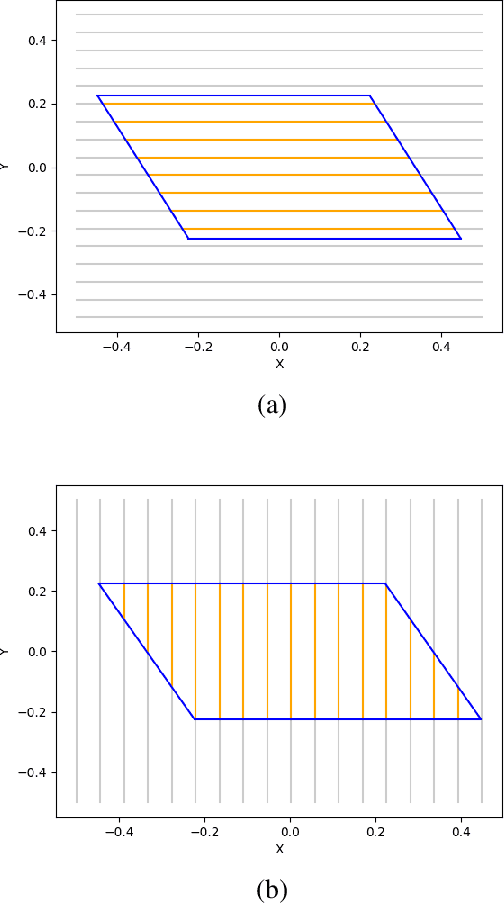
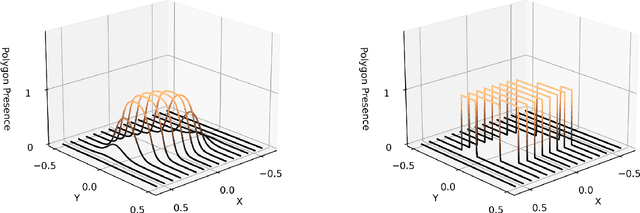
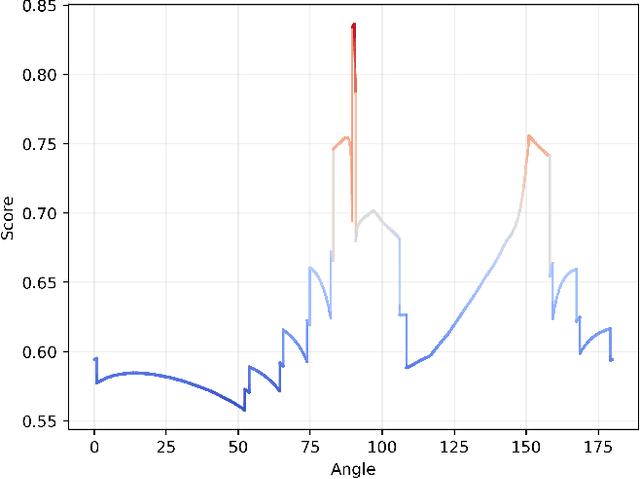
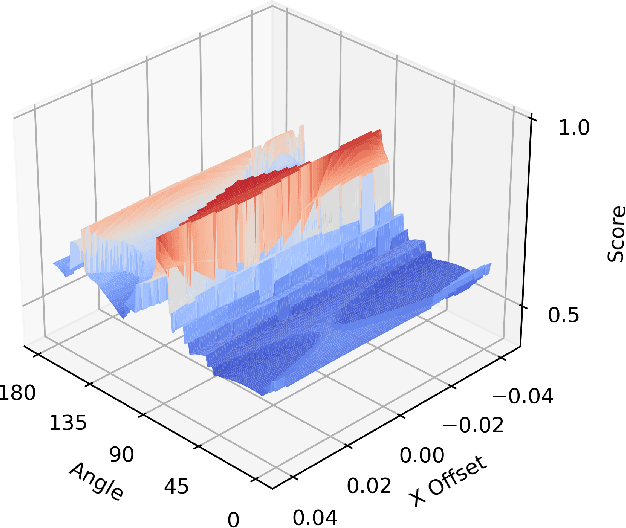
This paper introduces a differentiable representation for optimization of boustrophedon path plans in convex polygons, explores an additional parameter of these path plans that can be optimized, discusses the properties of this representation that can be leveraged during the optimization process, and shows that the previously published attempt at optimization of these path plans was too coarse to be practically useful. Experiments were conducted to show that this differentiable representation can reproduce the same scores from transitional discrete representations of boustrophedon path plans with high fidelity. Finally, optimization via gradient descent was attempted, but found to fail because the search space is far more non-convex than was previously considered in the literature. The wide range of applications for boustrophedon path plans means that this work has the potential to improve path planning efficiency in numerous areas of robotics including mapping and search tasks using uncrewed aerial systems, environmental sampling tasks using uncrewed marine vehicles, and agricultural tasks using ground vehicles, among numerous others applications.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge