Difference-in-Differences with Time-varying Continuous Treatments using Double/Debiased Machine Learning
Paper and Code
Oct 28, 2024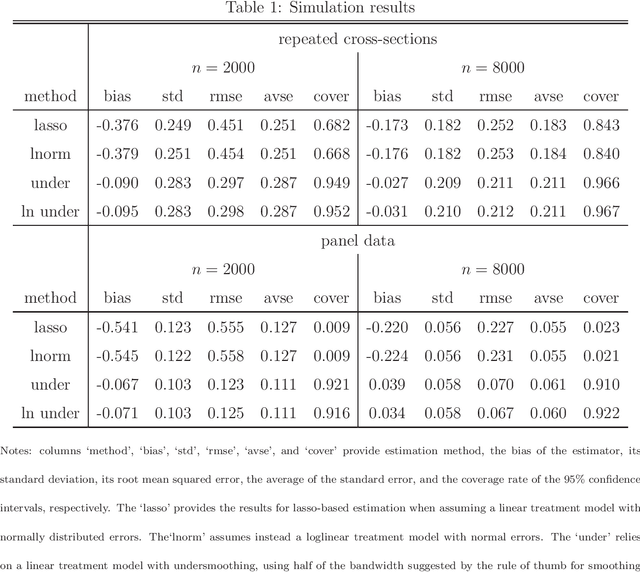
We propose a difference-in-differences (DiD) method for a time-varying continuous treatment and multiple time periods. Our framework assesses the average treatment effect on the treated (ATET) when comparing two non-zero treatment doses. The identification is based on a conditional parallel trend assumption imposed on the mean potential outcome under the lower dose, given observed covariates and past treatment histories. We employ kernel-based ATET estimators for repeated cross-sections and panel data adopting the double/debiased machine learning framework to control for covariates and past treatment histories in a data-adaptive manner. We also demonstrate the asymptotic normality of our estimation approach under specific regularity conditions. In a simulation study, we find a compelling finite sample performance of undersmoothed versions of our estimators in setups with several thousand observations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge