Dictionary Learning with Equiprobable Matching Pursuit
Paper and Code
Nov 28, 2016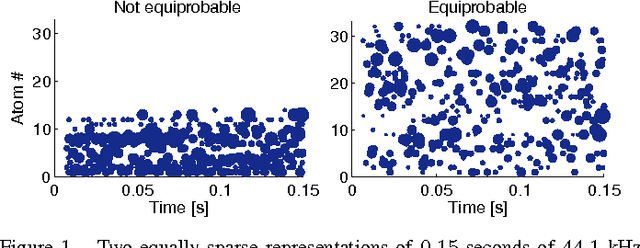
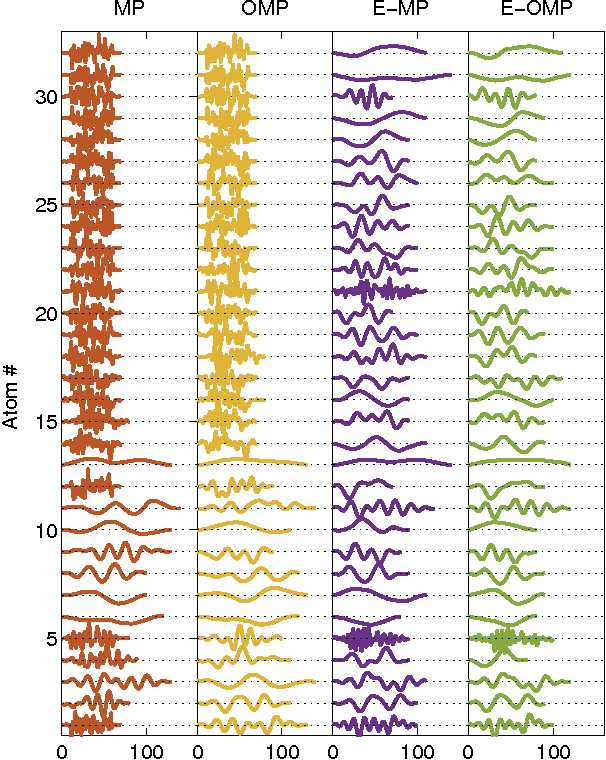
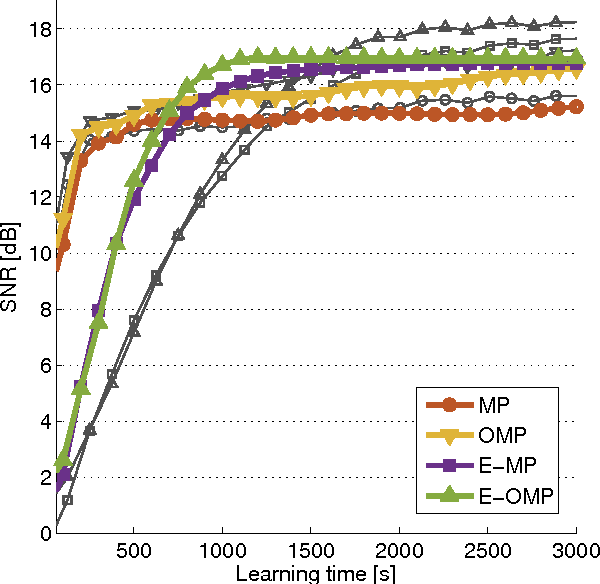
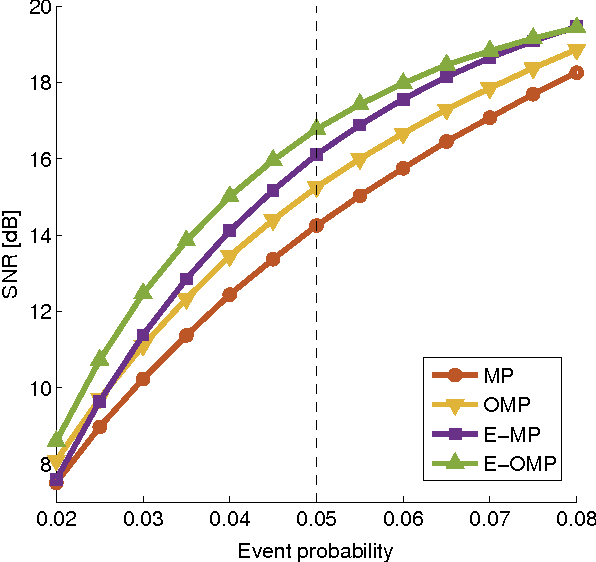
Sparse signal representations based on linear combinations of learned atoms have been used to obtain state-of-the-art results in several practical signal processing applications. Approximation methods are needed to process high-dimensional signals in this way because the problem to calculate optimal atoms for sparse coding is NP-hard. Here we study greedy algorithms for unsupervised learning of dictionaries of shift-invariant atoms and propose a new method where each atom is selected with the same probability on average, which corresponds to the homeostatic regulation of a recurrent convolutional neural network. Equiprobable selection can be used with several greedy algorithms for dictionary learning to ensure that all atoms adapt during training and that no particular atom is more likely to take part in the linear combination on average. We demonstrate via simulation experiments that dictionary learning with equiprobable selection results in higher entropy of the sparse representation and lower reconstruction and denoising errors, both in the case of ordinary matching pursuit and orthogonal matching pursuit with shift-invariant dictionaries. Furthermore, we show that the computational costs of the matching pursuits are lower with equiprobable selection, leading to faster and more accurate dictionary learning algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge