Deterministic Apple Tasting
Paper and Code
Oct 14, 2024
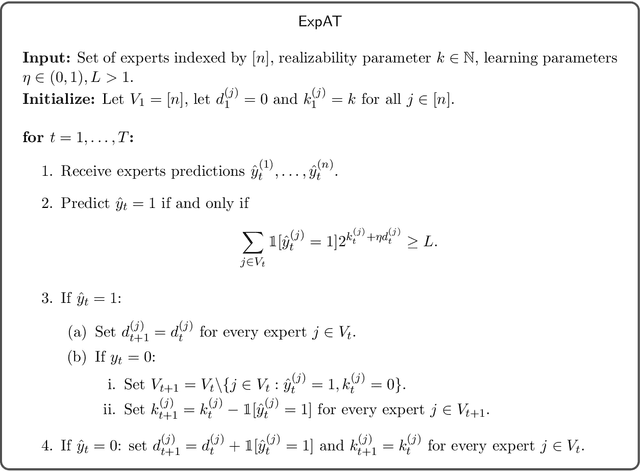


In binary ($0/1$) online classification with apple tasting feedback, the learner receives feedback only when predicting $1$. Besides some degenerate learning tasks, all previously known learning algorithms for this model are randomized. Consequently, prior to this work it was unknown whether deterministic apple tasting is generally feasible. In this work, we provide the first widely-applicable deterministic apple tasting learner, and show that in the realizable case, a hypothesis class is learnable if and only if it is deterministically learnable, confirming a conjecture of [Raman, Subedi, Raman, Tewari-24]. Quantitatively, we show that every class $\mathcal{H}$ is learnable with mistake bound $O \left(\sqrt{\mathtt{L}(\mathcal{H}) T \log T} \right)$ (where $\mathtt{L}(\mathcal{H})$ is the Littlestone dimension of $\mathcal{H}$), and that this is tight for some classes. We further study the agnostic case, in which the best hypothesis makes at most $k$ many mistakes, and prove a trichotomy stating that every class $\mathcal{H}$ must be either easy, hard, or unlearnable. Easy classes have (both randomized and deterministic) mistake bound $\Theta_{\mathcal{H}}(k)$. Hard classes have randomized mistake bound $\tilde{\Theta}_{\mathcal{H}} \left(k + \sqrt{T} \right)$, and deterministic mistake bound $\tilde{\Theta}_{\mathcal{H}} \left(\sqrt{k \cdot T} \right)$, where $T$ is the time horizon. Unlearnable classes have (both randomized and deterministic) mistake bound $\Theta(T)$. Our upper bound is based on a deterministic algorithm for learning from expert advice with apple tasting feedback, a problem interesting in its own right. For this problem, we show that the optimal deterministic mistake bound is $\Theta \left(\sqrt{T (k + \log n)} \right)$ for all $k$ and $T \leq n \leq 2^T$, where $n$ is the number of experts.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge