Determining Joint Periodicities in Multi-time Data With Sampling Uncertainties
Paper and Code
Oct 05, 2021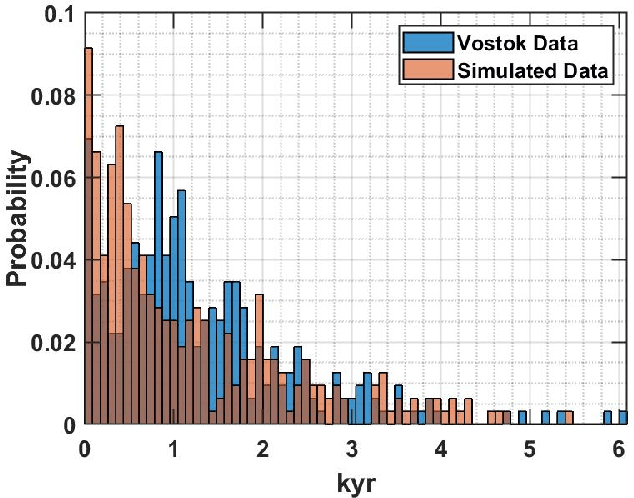
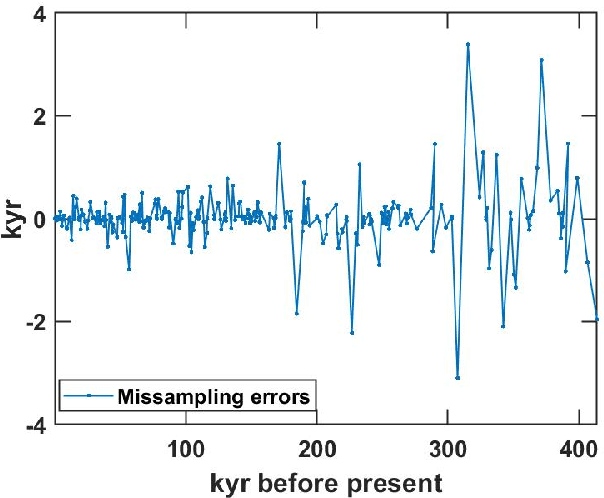
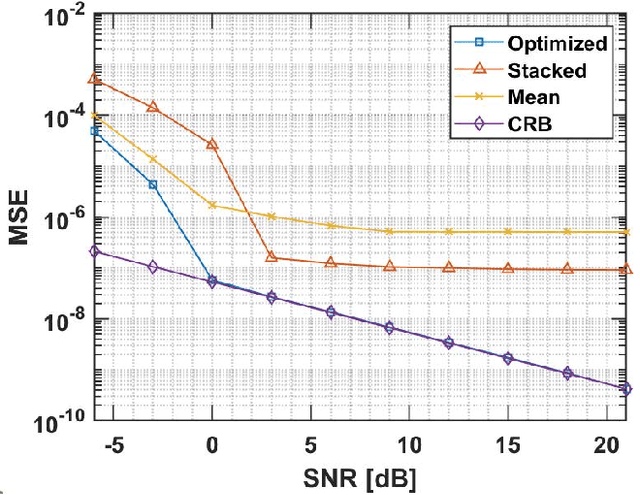
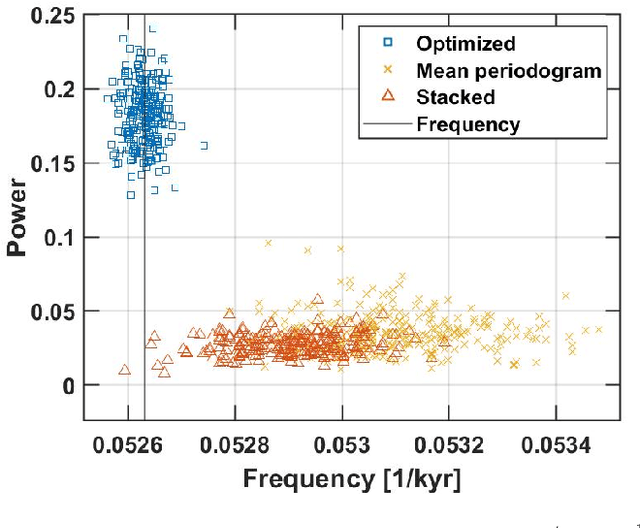
In this work, we introduce a novel approach for determining a joint sparse spectrum from several non-uniformly sampled data sets, where each data set is assumed to have its own, possibly disjoint, and only partially known, sampling times. The potential of the proposed approach is illustrated using a spectral estimation problem in paleoclimatology. In this problem, each data point derives from a separate ice core measurement, resulting in that even though all measurements reflect the same periodicities, the sampling times and phases differ among the data sets. In addition, sampling times are only approximately known. The resulting joint estimate exploiting all available data is formulated using a sparse reconstruction framework allowing for a reliable and robust estimate of the underlying periodicities. The corresponding misspecified Cram\'er-Rao lower bound, accounting for the expected sampling uncertainties, is derived and the proposed method is shown to attain the resulting bound when the signal to noise ratio is sufficiently high. The performance of the proposed method is illustrated as compared to other commonly used approaches using both simulated and measured ice core data sets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge