Detection in the stochastic block model with multiple clusters: proof of the achievability conjectures, acyclic BP, and the information-computation gap
Paper and Code
Sep 15, 2016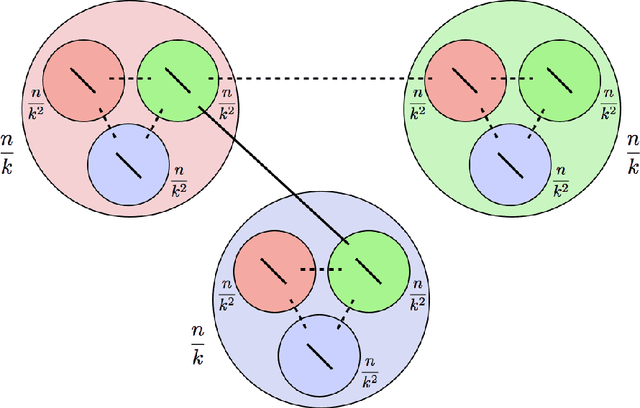
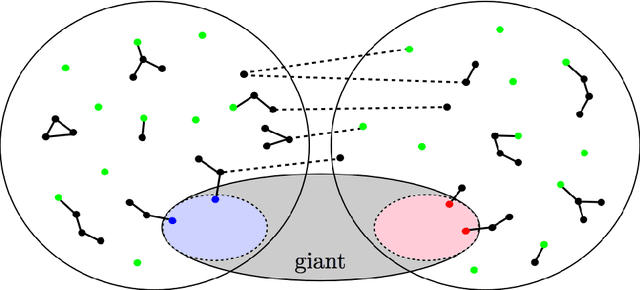
In a paper that initiated the modern study of the stochastic block model, Decelle et al., backed by Mossel et al., made the following conjecture: Denote by $k$ the number of balanced communities, $a/n$ the probability of connecting inside communities and $b/n$ across, and set $\mathrm{SNR}=(a-b)^2/(k(a+(k-1)b)$; for any $k \geq 2$, it is possible to detect communities efficiently whenever $\mathrm{SNR}>1$ (the KS threshold), whereas for $k\geq 4$, it is possible to detect communities information-theoretically for some $\mathrm{SNR}<1$. Massouli\'e, Mossel et al.\ and Bordenave et al.\ succeeded in proving that the KS threshold is efficiently achievable for $k=2$, while Mossel et al.\ proved that it cannot be crossed information-theoretically for $k=2$. The above conjecture remained open for $k \geq 3$. This paper proves this conjecture, further extending the efficient detection to non-symmetrical SBMs with a generalized notion of detection and KS threshold. For the efficient part, a linearized acyclic belief propagation (ABP) algorithm is developed and proved to detect communities for any $k$ down to the KS threshold in time $O(n \log n)$. Achieving this requires showing optimality of ABP in the presence of cycles, a challenge for message passing algorithms. The paper further connects ABP to a power iteration method with a nonbacktracking operator of generalized order, formalizing the interplay between message passing and spectral methods. For the information-theoretic (IT) part, a non-efficient algorithm sampling a typical clustering is shown to break down the KS threshold at $k=4$. The emerging gap is shown to be large in some cases; if $a=0$, the KS threshold reads $b \gtrsim k^2$ whereas the IT bound reads $b \gtrsim k \ln(k)$, making the SBM a good study-case for information-computation gaps.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge