Design of Capacity-Approaching Low-Density Parity-Check Codes using Recurrent Neural Networks
Paper and Code
Jan 05, 2020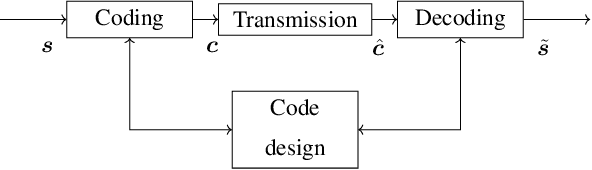
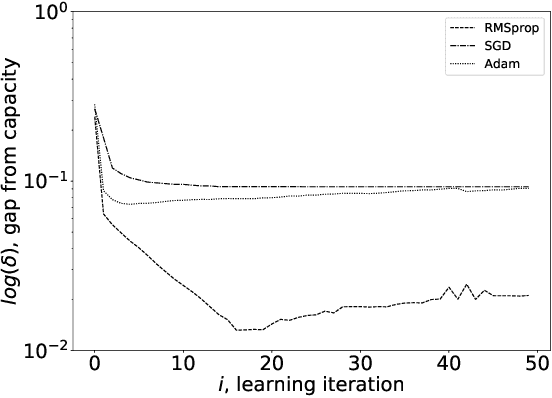
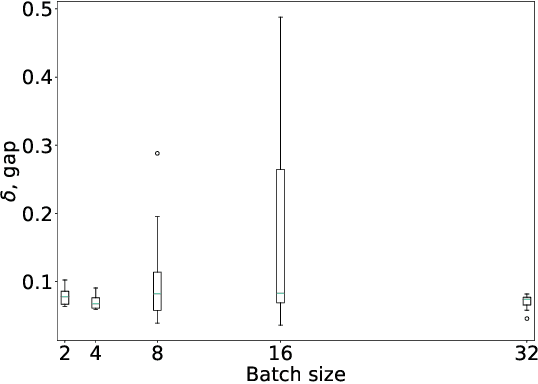
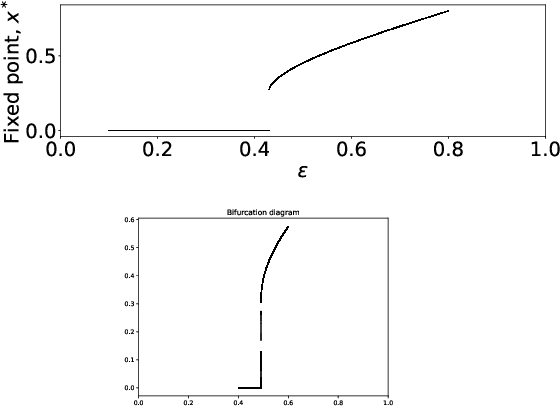
In this paper, we model Density Evolution (DE) using Recurrent Neural Networks (RNNs) with the aim of designing capacity-approaching Irregular Low-Density Parity-Check (LDPC) codes for binary erasure channels. In particular, we present a method for determining the coefficients of the degree distributions, characterizing the structure of an LDPC code. We refer to our RNN architecture as Neural Density Evolution (NDE) and determine the weights of the RNN that correspond to optimal designs by minimizing a loss function that enforces the properties of asymptotically optimal design, as well as the desired structural characteristics of the code. This renders the LDPC design process highly configurable, as constraints can be added to meet applications' requirements by means of modifying the loss function. In order to train the RNN, we generate data corresponding to the expected channel noise. We analyze the complexity and optimality of NDE theoretically, and compare it with traditional design methods that employ differential evolution. Simulations illustrate that NDE improves upon differential evolution both in terms of asymptotic performance and complexity. Although we focus on asymptotic settings, we evaluate designs found by NDE for finite codeword lengths and observe that performance remains satisfactory across a variety of channels.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge