DES: a Challenge Problem for Nonmonotonic Reasoning Systems
Paper and Code
Mar 08, 2000
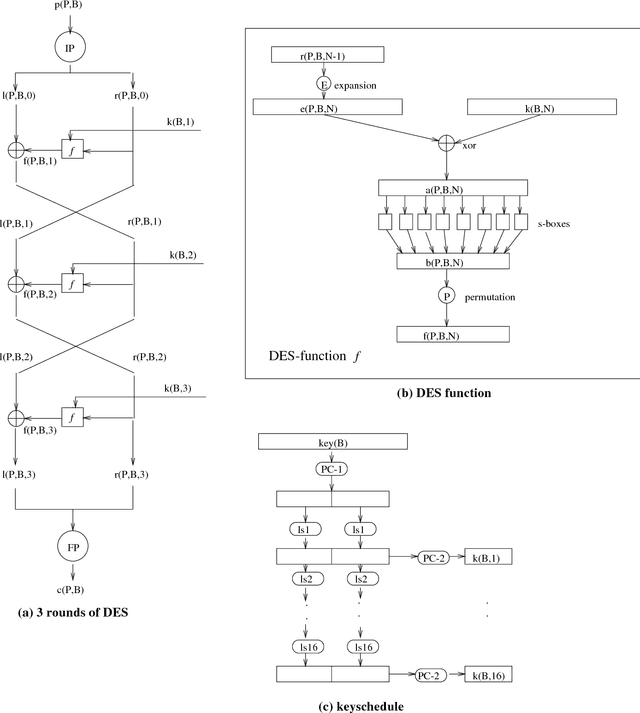
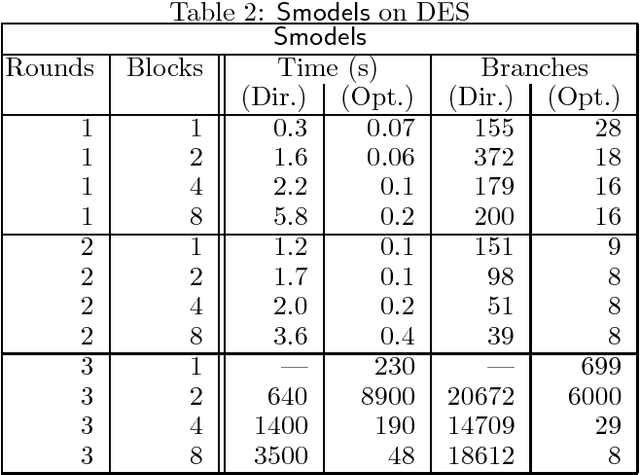

The US Data Encryption Standard, DES for short, is put forward as an interesting benchmark problem for nonmonotonic reasoning systems because (i) it provides a set of test cases of industrial relevance which shares features of randomly generated problems and real-world problems, (ii) the representation of DES using normal logic programs with the stable model semantics is simple and easy to understand, and (iii) this subclass of logic programs can be seen as an interesting special case for many other formalizations of nonmonotonic reasoning. In this paper we present two encodings of DES as logic programs: a direct one out of the standard specifications and an optimized one extending the work of Massacci and Marraro. The computational properties of the encodings are studied by using them for DES key search with the Smodels system as the implementation of the stable model semantics. Results indicate that the encodings and Smodels are quite competitive: they outperform state-of-the-art SAT-checkers working with an optimized encoding of DES into SAT and are comparable with a SAT-checker that is customized and tuned for the optimized SAT encoding.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge