Derivative-Free Optimization via Finite Difference Approximation: An Experimental Study

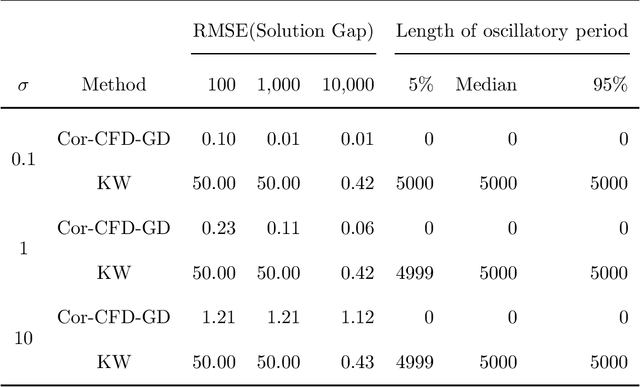
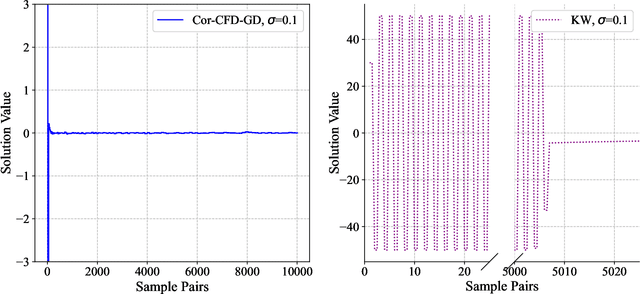
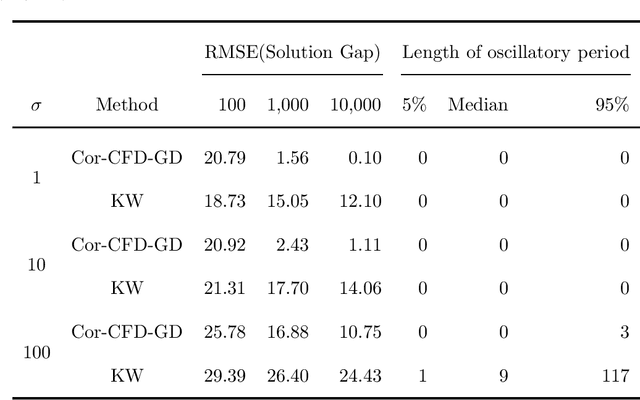
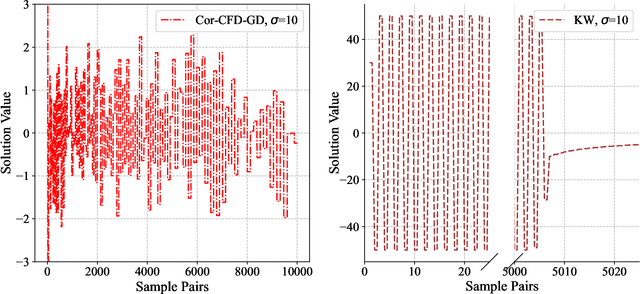
Derivative-free optimization (DFO) is vital in solving complex optimization problems where only noisy function evaluations are available through an oracle. Within this domain, DFO via finite difference (FD) approximation has emerged as a powerful method. Two classical approaches are the Kiefer-Wolfowitz (KW) and simultaneous perturbation stochastic approximation (SPSA) algorithms, which estimate gradients using just two samples in each iteration to conserve samples. However, this approach yields imprecise gradient estimators, necessitating diminishing step sizes to ensure convergence, often resulting in slow optimization progress. In contrast, FD estimators constructed from batch samples approximate gradients more accurately. While gradient descent algorithms using batch-based FD estimators achieve more precise results in each iteration, they require more samples and permit fewer iterations. This raises a fundamental question: which approach is more effective -- KW-style methods or DFO with batch-based FD estimators? This paper conducts a comprehensive experimental comparison among these approaches, examining the fundamental trade-off between gradient estimation accuracy and iteration steps. Through extensive experiments in both low-dimensional and high-dimensional settings, we demonstrate a surprising finding: when an efficient batch-based FD estimator is applied, its corresponding gradient descent algorithm generally shows better performance compared to classical KW and SPSA algorithms in our tested scenarios.