Deformable Graph Convolutional Networks
Paper and Code
Dec 29, 2021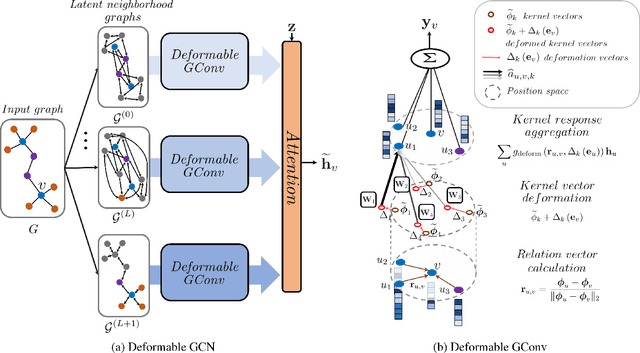
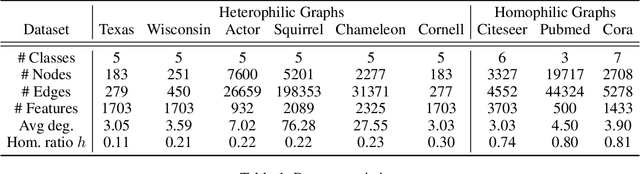
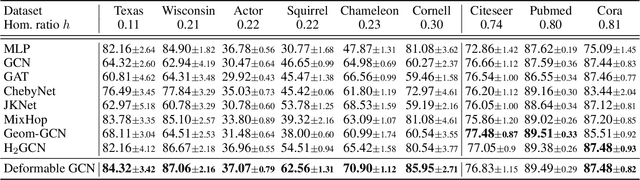
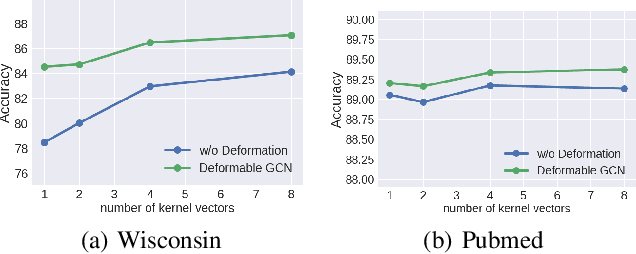
Graph neural networks (GNNs) have significantly improved the representation power for graph-structured data. Despite of the recent success of GNNs, the graph convolution in most GNNs have two limitations. Since the graph convolution is performed in a small local neighborhood on the input graph, it is inherently incapable to capture long-range dependencies between distance nodes. In addition, when a node has neighbors that belong to different classes, i.e., heterophily, the aggregated messages from them often negatively affect representation learning. To address the two common problems of graph convolution, in this paper, we propose Deformable Graph Convolutional Networks (Deformable GCNs) that adaptively perform convolution in multiple latent spaces and capture short/long-range dependencies between nodes. Separated from node representations (features), our framework simultaneously learns the node positional embeddings (coordinates) to determine the relations between nodes in an end-to-end fashion. Depending on node position, the convolution kernels are deformed by deformation vectors and apply different transformations to its neighbor nodes. Our extensive experiments demonstrate that Deformable GCNs flexibly handles the heterophily and achieve the best performance in node classification tasks on six heterophilic graph datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge