Deep Variational Koopman Models: Inferring Koopman Observations for Uncertainty-Aware Dynamics Modeling and Control
Paper and Code
Feb 26, 2019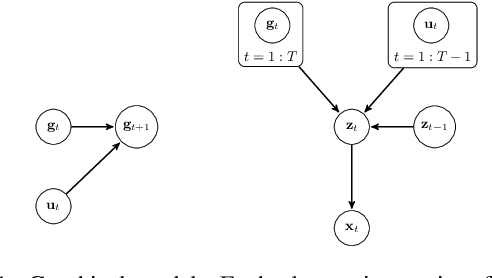
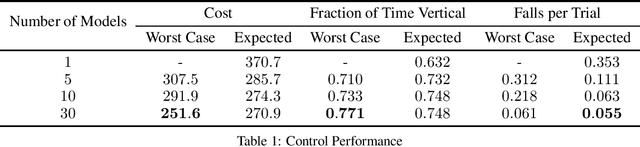
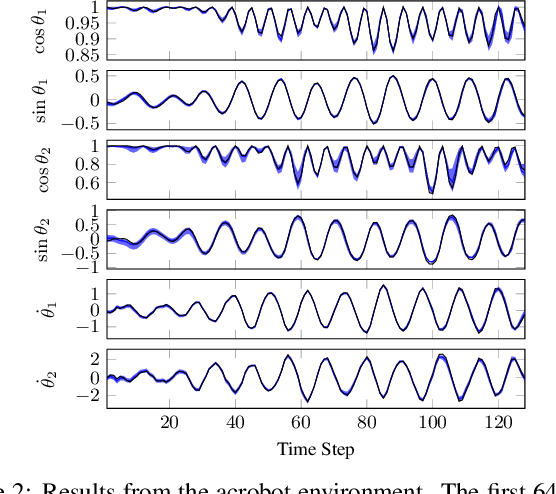

Koopman theory asserts that a nonlinear dynamical system can be mapped to a linear system, where the Koopman operator advances observations of the state forward in time. However, the observable functions that map states to observations are generally unknown. We introduce the Deep Variational Koopman (DVK) model, a method for inferring distributions over observations that can be propagated linearly in time. By sampling from the inferred distributions, we obtain a distribution over dynamical models, which in turn provides a distribution over possible outcomes as a modeled system advances in time. Experiments show that the DVK model is effective at long-term prediction for a variety of dynamical systems. Furthermore, we describe how to incorporate the learned models into a control framework, and demonstrate that accounting for the uncertainty present in the distribution over dynamical models enables more effective control.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge