Deep learning with t-exponential Bayesian kitchen sinks
Paper and Code
Feb 10, 2018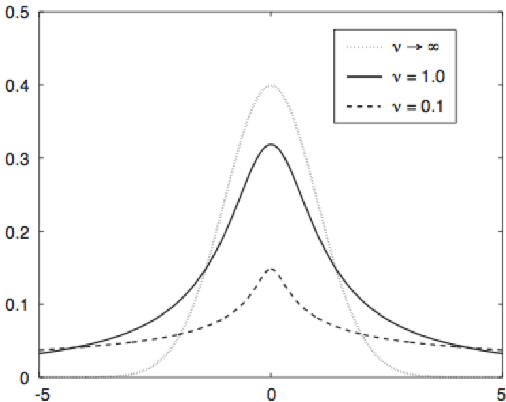
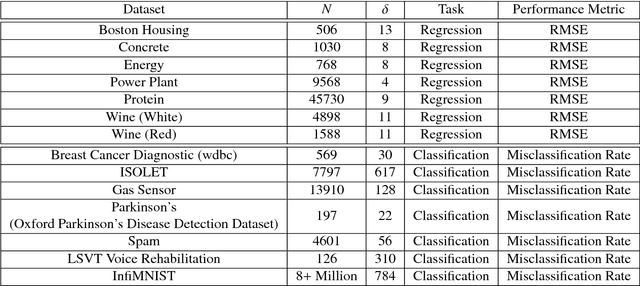
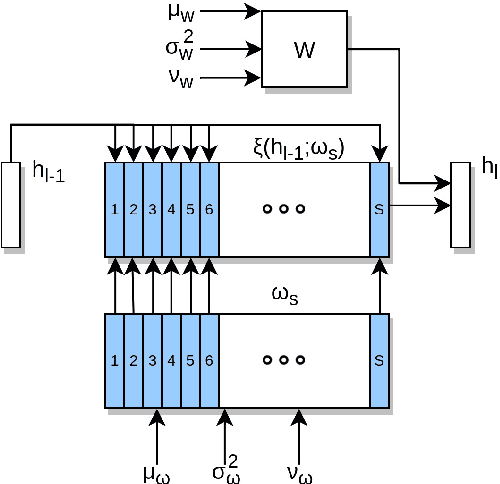
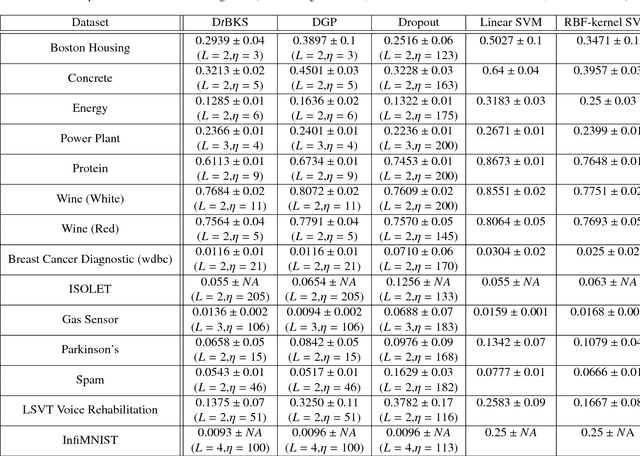
Bayesian learning has been recently considered as an effective means of accounting for uncertainty in trained deep network parameters. This is of crucial importance when dealing with small or sparse training datasets. On the other hand, shallow models that compute weighted sums of their inputs, after passing them through a bank of arbitrary randomized nonlinearities, have been recently shown to enjoy good test error bounds that depend on the number of nonlinearities. Inspired from these advances, in this paper we examine novel deep network architectures, where each layer comprises a bank of arbitrary nonlinearities, linearly combined using multiple alternative sets of weights. We effect model training by means of approximate inference based on a t-divergence measure; this generalizes the Kullback-Leibler divergence in the context of the t-exponential family of distributions. We adopt the t-exponential family since it can more flexibly accommodate real-world data, that entail outliers and distributions with fat tails, compared to conventional Gaussian model assumptions. We extensively evaluate our approach using several challenging benchmarks, and provide comparative results to related state-of-the-art techniques.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge