Deep learning neural networks for the third-order nonlinear Schrodinger equation: Solitons, breathers, and rogue waves
Paper and Code
Apr 30, 2021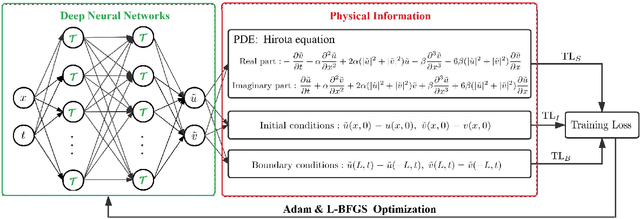

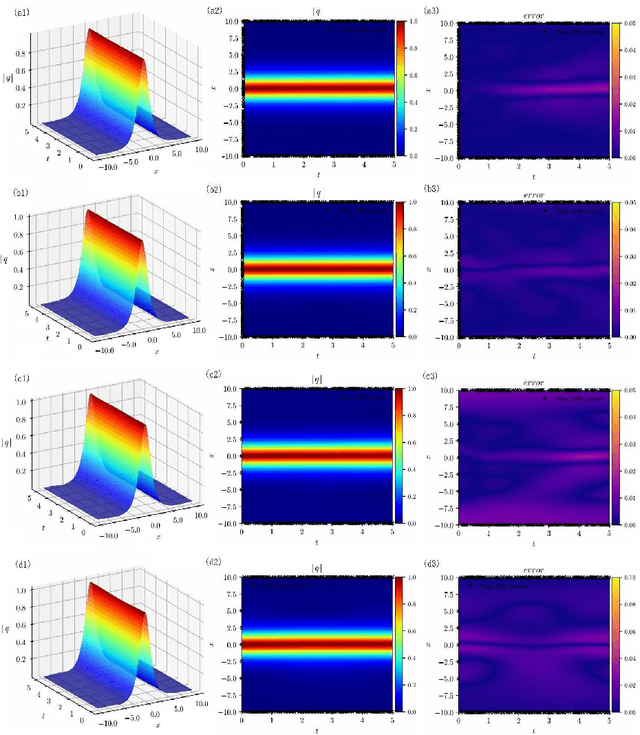

The third-order nonlinear Schrodinger equation (alias the Hirota equation) is investigated via deep leaning neural networks, which describes the strongly dispersive ion-acoustic wave in plasma and the wave propagation of ultrashort light pulses in optical fibers, as well as broader-banded waves on deep water. In this paper, we use the physics-informed neural networks (PINNs) deep learning method to explore the data-driven solutions (e.g., soliton, breather, and rogue waves) of the Hirota equation when the two types of the unperturbated and unperturbated (a 2% noise) training data are considered. Moreover, we use the PINNs deep learning to study the data-driven discovery of parameters appearing in the Hirota equation with the aid of solitons.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge