Deep Learning algorithms for solving high dimensional nonlinear Backward Stochastic Differential Equations

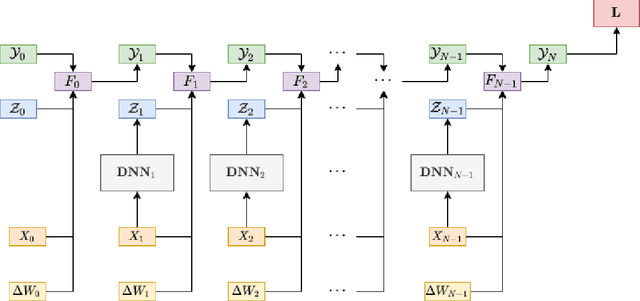
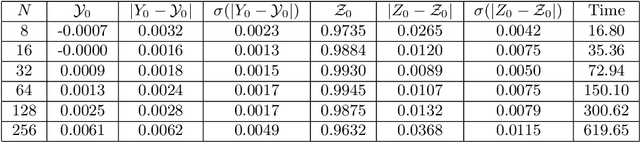
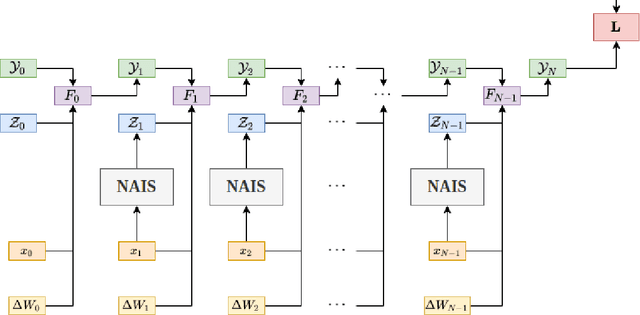
We study deep learning-based schemes for solving high dimensional nonlinear backward stochastic differential equations (BSDEs). First we show how to improve the performances of the proposed scheme in [W. E and J. Han and A. Jentzen, Commun. Math. Stat., 5 (2017), pp.349-380] regarding computational time and stability of numerical convergence by using the advanced neural network architecture instead of the stacked deep neural networks. Furthermore, the proposed scheme in that work can be stuck in local minima, especially for a complex solution structure and longer terminal time. To solve this problem, we investigate to reformulate the problem by including local losses and exploit the Long Short Term Memory (LSTM) networks which are a type of recurrent neural networks (RNN). Finally, in order to study numerical convergence and thus illustrate the improved performances with the proposed methods, we provide numerical results for several 100-dimensional nonlinear BSDEs including a nonlinear pricing problem in finance.