Deep calibration of rough stochastic volatility models
Paper and Code
Oct 08, 2018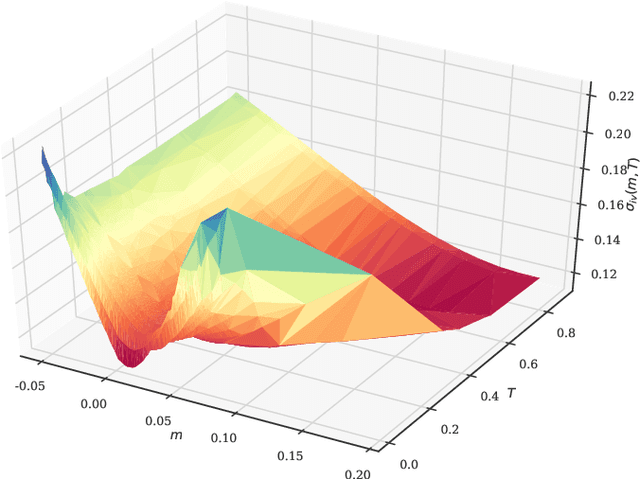
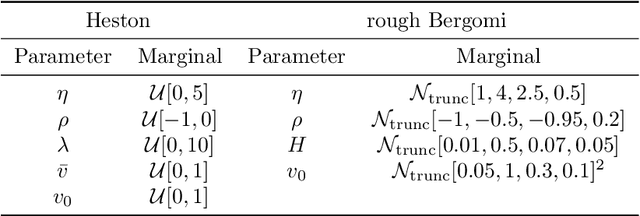
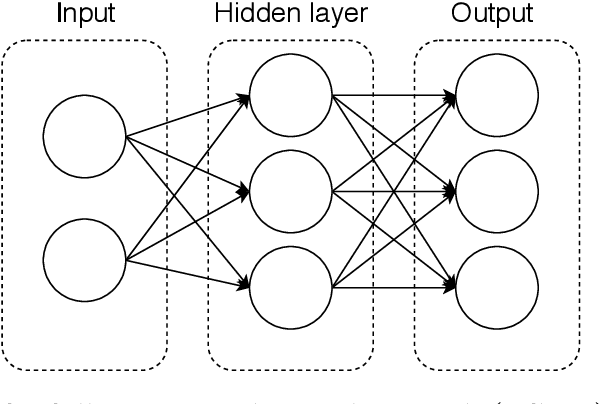
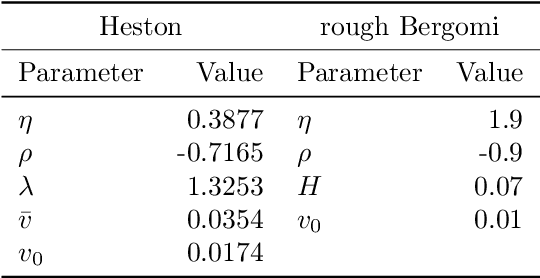
Sparked by Al\`os, Le\'on, and Vives (2007); Fukasawa (2011, 2017); Gatheral, Jaisson, and Rosenbaum (2018), so-called rough stochastic volatility models such as the rough Bergomi model by Bayer, Friz, and Gatheral (2016) constitute the latest evolution in option price modeling. Unlike standard bivariate diffusion models such as Heston (1993), these non-Markovian models with fractional volatility drivers allow to parsimoniously recover key stylized facts of market implied volatility surfaces such as the exploding power-law behaviour of the at-the-money volatility skew as time to maturity goes to zero. Standard model calibration routines rely on the repetitive evaluation of the map from model parameters to Black-Scholes implied volatility, rendering calibration of many (rough) stochastic volatility models prohibitively expensive since there the map can often only be approximated by costly Monte Carlo (MC) simulations (Bennedsen, Lunde, & Pakkanen, 2017; McCrickerd & Pakkanen, 2018; Bayer et al., 2016; Horvath, Jacquier, & Muguruza, 2017). As a remedy, we propose to combine a standard Levenberg-Marquardt calibration routine with neural network regression, replacing expensive MC simulations with cheap forward runs of a neural network trained to approximate the implied volatility map. Numerical experiments confirm the high accuracy and speed of our approach.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge