Decentralized Heading Control with Rate Constraints using Pulse-Coupled Oscillators

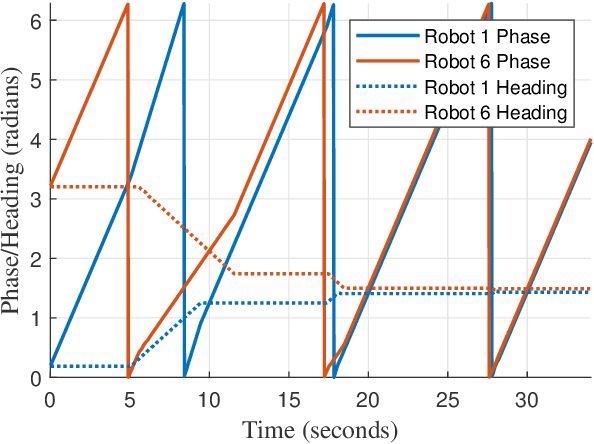
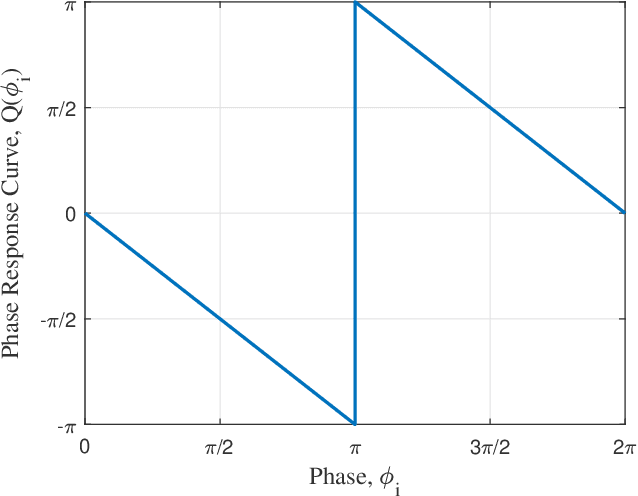
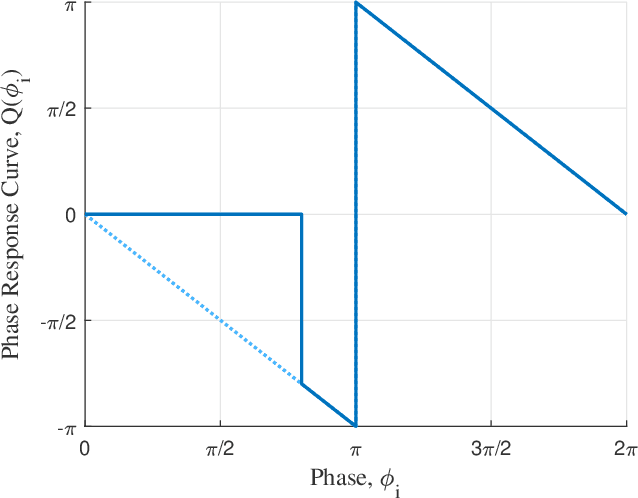
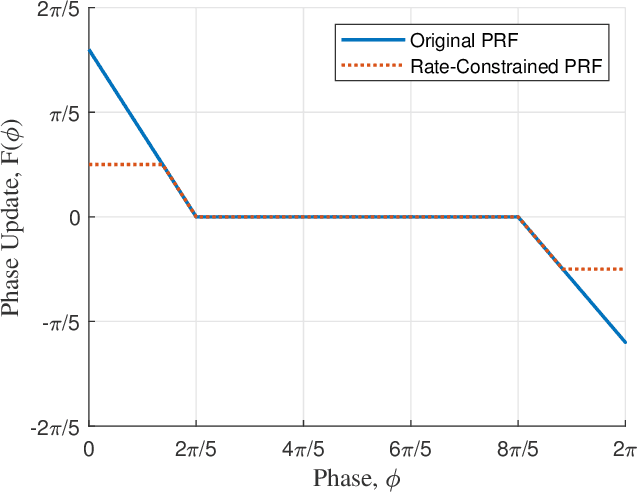
Decentralized heading control is crucial for robotic network operations such as surveillance, exploration, and cooperative construction. However, few results consider decentralized heading control when the speed of heading adjustment is restricted. In this paper, we propose a simple hybrid-dynamical model based on pulse-coupled oscillators for decentralized heading control in mobile robots while accounting for the constraint on the rate of heading change. The pulse-coupled oscillator model is effective in coordinating the phase of oscillator networks and hence is promising for robotic heading coordination given that both phase and heading evolve on the same one-dimensional torus. However, existing pulse-coupled oscillator results require the phase adjustment to be instantaneous, which cannot hold for robot heading adjustment due to physical limitations. We propose a generalization to the standard pulse-coupled oscillator model to allow for the phase to adjust at a finite rate, yet still have the oscillator network converge to the desired state, making our approach applicable to robotic heading coordination under rate constraints. We provide rigorous mathematical proof for the achievement of both synchronized and desynchronized heading relationships, and experimentally verify the results using extensive tests on a multi-robot platform.