DDE-Find: Learning Delay Differential Equations from Data

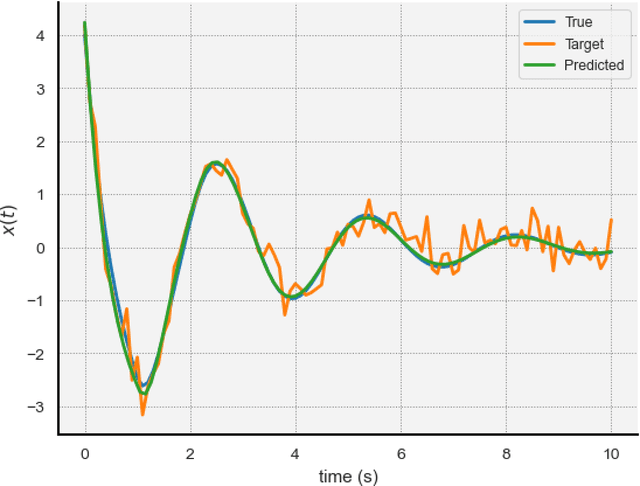
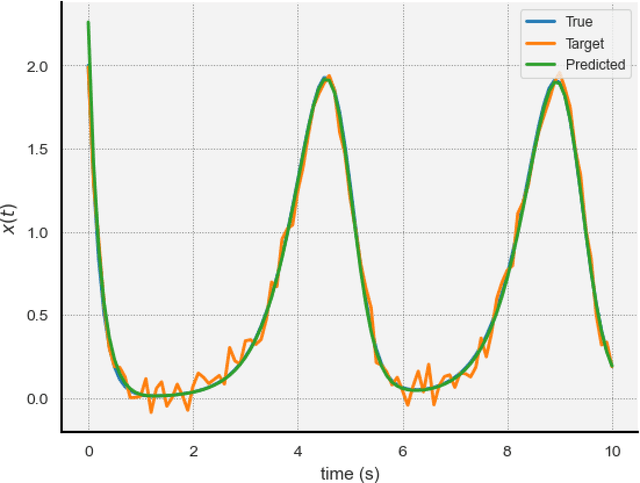
Delay Differential Equations (DDEs) are a class of differential equations that can model diverse scientific phenomena. However, identifying the parameters, especially the time delay, that make a DDE's predictions match experimental results can be challenging. We introduce DDE-Find, a data-driven framework for learning a DDE's parameters, time delay, and initial condition function. DDE-Find uses an adjoint-based approach to efficiently compute the gradient of a loss function with respect to the model parameters. We motivate and rigorously prove an expression for the gradients of the loss using the adjoint. DDE-Find builds upon recent developments in learning DDEs from data and delivers the first complete framework for learning DDEs from data. Through a series of numerical experiments, we demonstrate that DDE-Find can learn DDEs from noisy, limited data.