Data-driven Abstractions with Probabilistic Guarantees for Linear PETC Systems
Paper and Code
Mar 10, 2022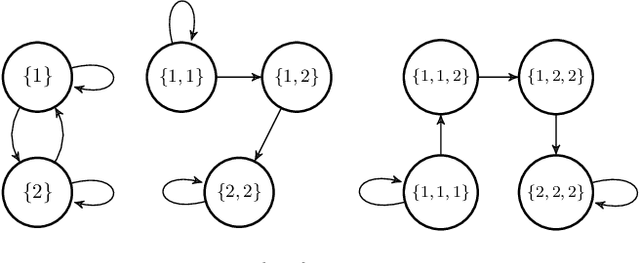
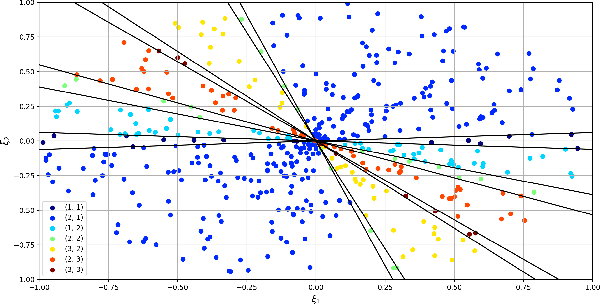
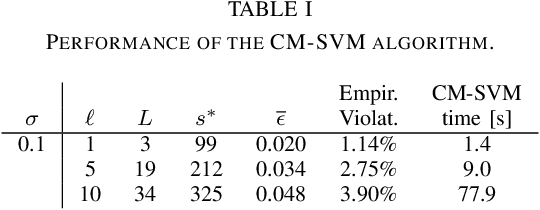
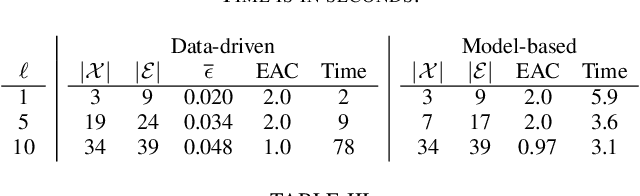
We employ the scenario approach to compute probably approximately correct (PAC) bounds on the average inter-sample time (AIST) generated by an unknown PETC system, based on a finite number of samples. We extend the scenario approach to multiclass SVM algorithms in order to construct a PAC map between the concrete, unknown state-space and the inter-sample times. We then build a traffic model applying an $\ell$-complete relation and find, in the underlying graph, the cycles of minimum and maximum average weight: these provide lower and upper bounds on the AIST. Numerical benchmarks show the practical applicability of our method, which is compared against model-based state-of-the-art tools.
* 6 pages
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge