Data Clustering via Principal Direction Gap Partitioning
Paper and Code
Nov 17, 2012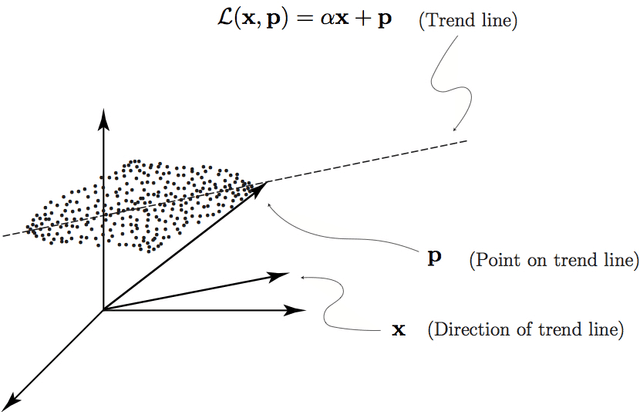
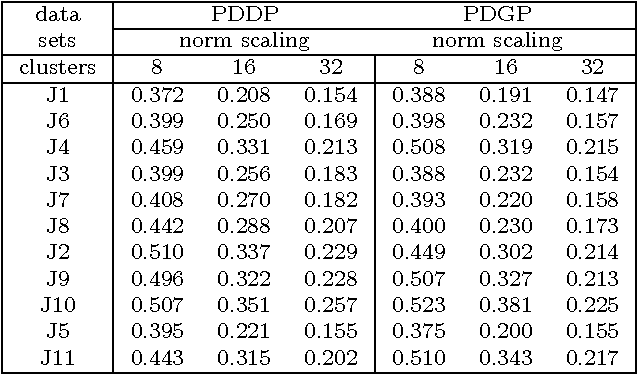
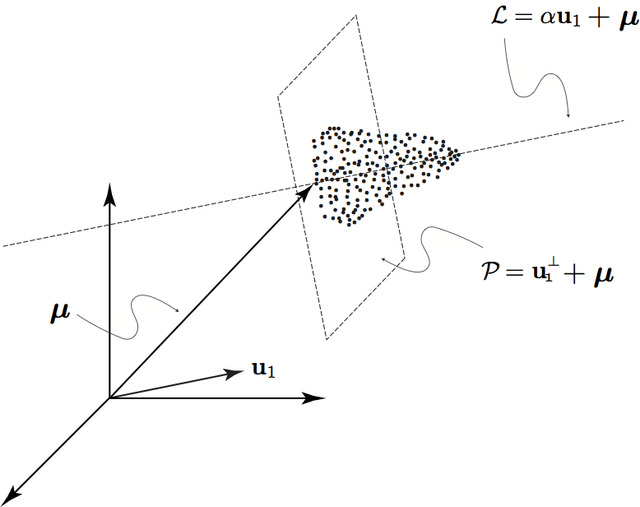
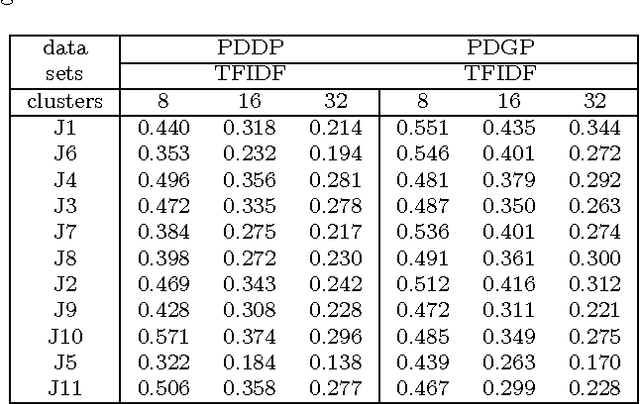
We explore the geometrical interpretation of the PCA based clustering algorithm Principal Direction Divisive Partitioning (PDDP). We give several examples where this algorithm breaks down, and suggest a new method, gap partitioning, which takes into account natural gaps in the data between clusters. Geometric features of the PCA space are derived and illustrated and experimental results are given which show our method is comparable on the datasets used in the original paper on PDDP.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge